题目内容
已知椭圆C1的中心在原点、焦点在x轴上,抛物线C2的顶点在原点、焦点在x轴上。小明从曲线C1,C2上各取若干个点(每条曲线上至少取两个点),并记录其坐标(x,y)。由于记录失误,使得其中恰好有一个点既不在椭圆上C1上,也不在抛物线C2上。小明的记录如下:
 据此,可推断椭圆C1的方程为 .
据此,可推断椭圆C1的方程为 .
【答案】
 +
+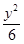 =1
=1
【解析】解:因为设抛物线C2:y2=2px(p≠0),由题意知C2:y2=4x,再设出椭圆的方程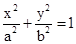 ,经过验证(-2,2)(0,
,经过验证(-2,2)(0,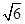 )在椭圆上可知椭圆的方程为
)在椭圆上可知椭圆的方程为 +
+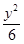 =1
=1

练习册系列答案
相关题目
 已知椭圆C1的中心在原点,离心率为
已知椭圆C1的中心在原点,离心率为