题目内容
(12分)设函数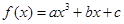
 为奇函数,其图象在x=1处的切线与直线
为奇函数,其图象在x=1处的切线与直线 垂直,导函数
垂直,导函数 的最小值为
的最小值为 .
.
(I)求 ;
;
(II)求函数 的单调递增区间,并求函数
的单调递增区间,并求函数 在
在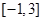 上的最大值和最小值.
上的最大值和最小值.
【答案】
(1)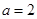 ,
,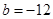 ,
,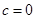 .
.
(2)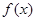 在
在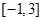 上的最大值是
上的最大值是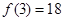 ,最小值是
,最小值是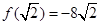
【解析】解: (Ⅰ)∵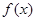 为奇函数,∴
为奇函数,∴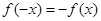
即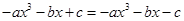 ∴
∴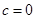 …………1分
…………1分
∵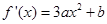 的最小值为
的最小值为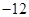 ,
,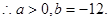 …………3分
…………3分
又直线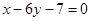 的斜率为
的斜率为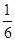
因此,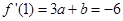 …………5分
…………5分
∴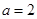 ,
,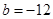 ,
,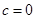 .
…………6分
.
…………6分
(Ⅱ) .
.
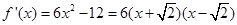 ,列表如下:
,列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
↗ |
极大 |
↘ |
极小 |
↗ |
所以函数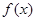 的单调增区间是
的单调增区间是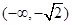 和
和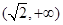 . …………9分
. …………9分
∵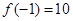 ,
,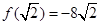 ,
,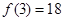
∴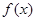 在
在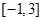 上的最大值是
上的最大值是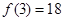 ,最小值是
,最小值是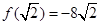 .……12分
.……12分

练习册系列答案
相关题目
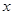
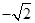
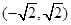
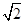
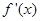

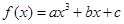
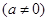 为奇函数,其图象在点
为奇函数,其图象在点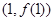 处的切线与直线
处的切线与直线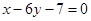 垂直,导函数
垂直,导函数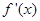 的最小值为
的最小值为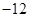 .试求
.试求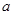 ,
, ,
,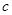 的值。
的值。
 为奇函数,其图象在点
为奇函数,其图象在点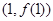 处的切线与直线
处的切线与直线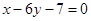 垂直,导函数
垂直,导函数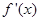 的最小值为
的最小值为 .
.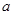 ,
, ,
, 的值;
的值;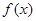 的单调递增区间,并求函数
的单调递增区间,并求函数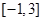 上的最大值和最小值.
上的最大值和最小值.