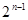题目内容
设数列的通项公式为an=2n-7,则|a1|+|a2|+…+|a15|=( )
分析:令an=2n-7≥0,解得n≥
.可知:从第4项开始大于0,|a1|+|a2|+…+|a15|=-a1-a2-a3+a4+a5+…+a15,利用等差数列的前n项和公式即可得出.
| 7 |
| 2 |
解答:解:令an=2n-7≥0,解得n≥
.
∴从第4项开始大于0,
∴|a1|+|a2|+…+|a15|=-a1-a2-a3+a4+a5+…+a15=5+3+1+1+3+…+(2×15-7)
=9+
=153.
故选A.
| 7 |
| 2 |
∴从第4项开始大于0,
∴|a1|+|a2|+…+|a15|=-a1-a2-a3+a4+a5+…+a15=5+3+1+1+3+…+(2×15-7)
=9+
| 12×(1+23) |
| 2 |
故选A.
点评:本题考查了含绝对值符号的数列求和、等差数列的前n项和公式等基础知识与基本技能方法,属于基础题.

练习册系列答案
相关题目
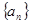 的通项公式为
的通项公式为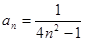 ,则
,则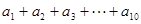 等于( )
等于( )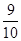 B.
B.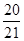 C.
C. 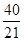 D.
D.
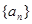 满足
满足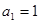 ,且对任意的
,且对任意的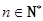 ,点
,点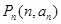 都有
都有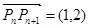 ,则数列
,则数列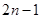 B.
B.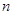 C.
C.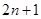 D.
D.