题目内容
某外商计划在4个候选城市中投资3个不同的项目，且在同一个城市投资的项目不超过2个，则该外商不同的投资方案有 ( )
| A．16种 | B．36种 | C．42种 | D．60种 |
D
解析试题分析：根据题意，分两种情况讨论，一是在两个城市分别投资1个项目、2个项目，二是在三个城市各投资1个项目，分别计算其情况数目，进而由加法原理，计算可得答案解：某外商计划在4个候选城市投资3个不同的项目，且在同一个城市投资的项目不超过2个，则有两种情况，一是在两个城市分别投资1个项目、2个项目，此时有
=36种方案，二是在三个城市各投资1个项目，有
=24种方案，共计有60种方案，故选D．
考点：排列组合的运用
点评：本题考查排列、组合的综合应用，要根据题意，认真分析，确定分类的依据，进而做到分类不重不漏．
练习册系列答案
相关题目
若
则
（ ）
A． | B． | C． | D． |
种 
种 
种 
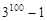种 从5位同学中选派4位同学在星期五、星期六、星期日参加公益活动，每人一天，要求星期五有2人参加，星期六、星期日各有1人参加，则不同的选派方法共有（ ）
| A．40种 | B．60种 | C．100种 | D．120种 |
现有排成一排的7个座位，安排3名同学就座，如果要求剩余的4个座位连在一起，那么不同的坐法总数为（ ）
| A．16 | B．18 | C．24 | D．32 |
将5名实习老师全部分配到高三年级的3个班实习，每班至少1名，最多2名，则不同的分配方案有（ ）
| A．30种 | B．90种 | C．180种 | D．270种 |
将3个不同的小球放入4个盒子中，则不同放法种数有（ ）
| A．81 | B．64 | C．2 | D．14 |
如图所示是某个区域的街道示意图（每个小矩形的边表示街道），则从A到B的最短线路有（ ）条
| A．24 | B．60 | C．84 | D．120 |