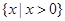题目内容
若函数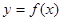 在
在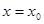 处取得极大值或极小值,则称
处取得极大值或极小值,则称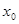 为函数
为函数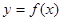 的极值点。已知
的极值点。已知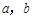 是实数,1和
是实数,1和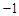 是函数
是函数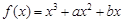 的两个极值点.
的两个极值点.
(1)求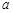 和
和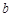 的值;
的值;
(2)设函数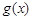 的导函数
的导函数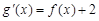 ,求
,求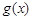 的极值点;
的极值点;
(3)设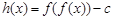 ,其中
,其中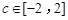 ,求函数
,求函数 的零点个数.
的零点个数.
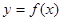 在
在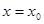 处取得极大值或极小值,则称
处取得极大值或极小值,则称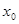 为函数
为函数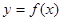 的极值点。已知
的极值点。已知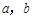 是实数,1和
是实数,1和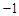 是函数
是函数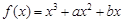 的两个极值点.
的两个极值点.(1)求
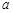 和
和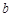 的值;
的值;(2)设函数
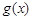 的导函数
的导函数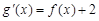 ,求
,求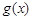 的极值点;
的极值点;(3)设
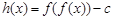 ,其中
,其中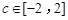 ,求函数
,求函数 的零点个数.
的零点个数.(1)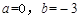
(2)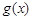 的极值点是-2
的极值点是-2
(3)当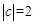 时,函数
时,函数 有5 个零点;当
有5 个零点;当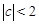 时,函数
时,函数 有9 个零点。
有9 个零点。
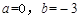
(2)
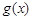 的极值点是-2
的极值点是-2(3)当
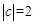 时,函数
时,函数 有5 个零点;当
有5 个零点;当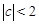 时,函数
时,函数 有9 个零点。
有9 个零点。(1)求出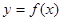 的导数,根据1和
的导数,根据1和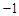 是函数
是函数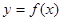 的两个极值点代入列方程组求解即可。
的两个极值点代入列方程组求解即可。
(2)由(1)得,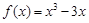 ,求出
,求出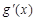 ,令
,令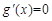 ,求解讨论即可。
,求解讨论即可。
(3)比较复杂,先分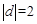 和
和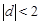 讨论关于
讨论关于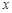 的方程
的方程 根的情况;再考虑函数
根的情况;再考虑函数 的零点
的零点
解:(1)由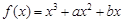 ,得
,得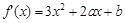 。
。
∵1和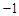 是函数
是函数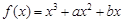 的两个极值点,
的两个极值点,
∴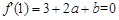 ,
,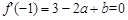 ,解得
,解得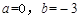 。
。
(2)∵ 由(1)得,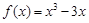 ,
,
∴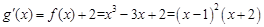 ,解得
,解得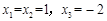 。
。
∵当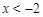 时,
时,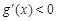 ;当
;当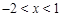 时,
时,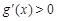 ,
,
∴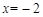 是
是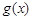 的极值点。
的极值点。
∵当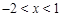 或
或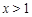 时,
时,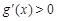 ,∴
,∴ 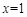 不是
不是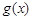 的极值点。
的极值点。
∴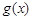 的极值点是-2。
的极值点是-2。
(3)令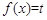 ,则
,则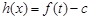 。
。
先讨论关于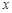 的方程
的方程 根的情况:
根的情况: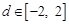
当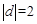 时,由(2 )可知,
时,由(2 )可知,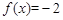 的两个不同的根为I 和一2 ,注意到
的两个不同的根为I 和一2 ,注意到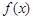 是奇函数,∴
是奇函数,∴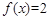 的两个不同的根为一和2。
的两个不同的根为一和2。
当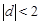 时,∵
时,∵ ,
,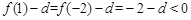 ,
,
∴一2 , -1,1 ,2 都不是 的根。
的根。
由(1)知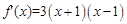 。
。
① 当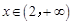 时,
时,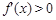 ,于是
,于是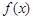 是单调增函数,从而
是单调增函数,从而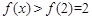 。
。
此时 在
在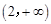 无实根。
无实根。
② 当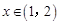 时.
时.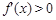 ,于是
,于是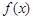 是单调增函数。
是单调增函数。
又∵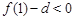 ,
,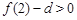 ,
,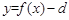 的图象不间断,
的图象不间断,
∴ 在(1 , 2 )内有唯一实根。
在(1 , 2 )内有唯一实根。
同理, 在(一2 ,一I )内有唯一实根。
在(一2 ,一I )内有唯一实根。
③ 当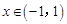 时,
时,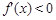 ,于是
,于是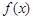 是单调减两数。
是单调减两数。
又∵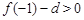 ,
, 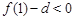 ,
,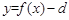 的图象不间断,
的图象不间断,
∴ 在(一1,1 )内有唯一实根。
在(一1,1 )内有唯一实根。
因此,当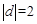 时,
时, 有两个不同的根
有两个不同的根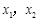 满足
满足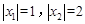 ;当
;当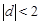 时
时
 有三个不同的根
有三个不同的根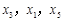 ,满足
,满足 。
。
现考虑函数 的零点:
的零点:
( i )当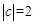 时,
时,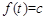 有两个根
有两个根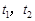 ,满足
,满足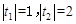 。
。
而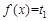 有三个不同的根,
有三个不同的根,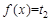 有两个不同的根,故
有两个不同的根,故 有5 个零点。
有5 个零点。
( 11 )当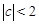 时,
时,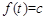 有三个不同的根
有三个不同的根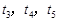 ,满足
,满足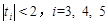 。
。
而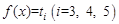 有三个不同的根,故
有三个不同的根,故 有9 个零点。
有9 个零点。
综上所述,当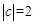 时,函数
时,函数 有5 个零点;当
有5 个零点;当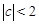 时,函数
时,函数 有9 个零点
有9 个零点
【考点定位】本题综合考查导数的定义、计算及其在求解函数极值和最值中的应用,考查较全面系统,要注意变形的等价性和函数零点的认识、极值和极值点的理解。本题主要考查数形结合思想和分类讨论思想,属于中高档试题,难度中等偏上,考查知识比较综合,全方位考查分析问题和解决问题的能力,运算量比较大。
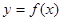 的导数,根据1和
的导数,根据1和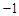 是函数
是函数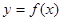 的两个极值点代入列方程组求解即可。
的两个极值点代入列方程组求解即可。(2)由(1)得,
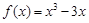 ,求出
,求出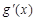 ,令
,令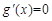 ,求解讨论即可。
,求解讨论即可。(3)比较复杂,先分
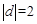 和
和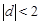 讨论关于
讨论关于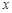 的方程
的方程 根的情况;再考虑函数
根的情况;再考虑函数 的零点
的零点解:(1)由
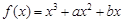 ,得
,得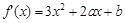 。
。∵1和
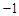 是函数
是函数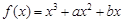 的两个极值点,
的两个极值点,∴
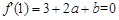 ,
,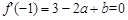 ,解得
,解得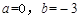 。
。(2)∵ 由(1)得,
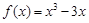 ,
,∴
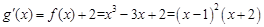 ,解得
,解得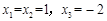 。
。∵当
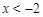 时,
时,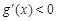 ;当
;当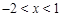 时,
时,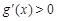 ,
,∴
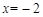 是
是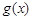 的极值点。
的极值点。∵当
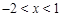 或
或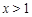 时,
时,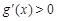 ,∴
,∴ 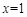 不是
不是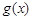 的极值点。
的极值点。∴
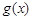 的极值点是-2。
的极值点是-2。(3)令
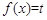 ,则
,则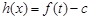 。
。先讨论关于
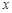 的方程
的方程 根的情况:
根的情况: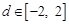
当
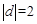 时,由(2 )可知,
时,由(2 )可知,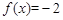 的两个不同的根为I 和一2 ,注意到
的两个不同的根为I 和一2 ,注意到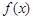 是奇函数,∴
是奇函数,∴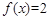 的两个不同的根为一和2。
的两个不同的根为一和2。当
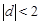 时,∵
时,∵ ,
,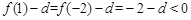 ,
,∴一2 , -1,1 ,2 都不是
 的根。
的根。由(1)知
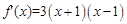 。
。① 当
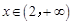 时,
时,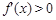 ,于是
,于是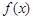 是单调增函数,从而
是单调增函数,从而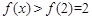 。
。此时
 在
在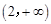 无实根。
无实根。② 当
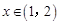 时.
时.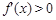 ,于是
,于是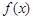 是单调增函数。
是单调增函数。又∵
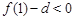 ,
,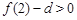 ,
,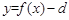 的图象不间断,
的图象不间断,∴
 在(1 , 2 )内有唯一实根。
在(1 , 2 )内有唯一实根。同理,
 在(一2 ,一I )内有唯一实根。
在(一2 ,一I )内有唯一实根。③ 当
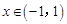 时,
时,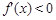 ,于是
,于是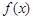 是单调减两数。
是单调减两数。又∵
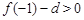 ,
, 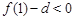 ,
,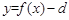 的图象不间断,
的图象不间断,∴
 在(一1,1 )内有唯一实根。
在(一1,1 )内有唯一实根。因此,当
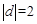 时,
时, 有两个不同的根
有两个不同的根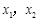 满足
满足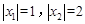 ;当
;当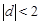 时
时 有三个不同的根
有三个不同的根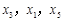 ,满足
,满足 。
。现考虑函数
 的零点:
的零点:( i )当
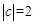 时,
时,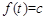 有两个根
有两个根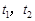 ,满足
,满足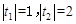 。
。而
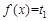 有三个不同的根,
有三个不同的根,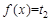 有两个不同的根,故
有两个不同的根,故 有5 个零点。
有5 个零点。( 11 )当
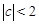 时,
时,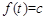 有三个不同的根
有三个不同的根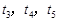 ,满足
,满足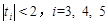 。
。而
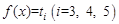 有三个不同的根,故
有三个不同的根,故 有9 个零点。
有9 个零点。综上所述,当
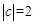 时,函数
时,函数 有5 个零点;当
有5 个零点;当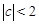 时,函数
时,函数 有9 个零点
有9 个零点【考点定位】本题综合考查导数的定义、计算及其在求解函数极值和最值中的应用,考查较全面系统,要注意变形的等价性和函数零点的认识、极值和极值点的理解。本题主要考查数形结合思想和分类讨论思想,属于中高档试题,难度中等偏上,考查知识比较综合,全方位考查分析问题和解决问题的能力,运算量比较大。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的图象是
的图象是
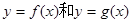 的定义域及值域均为
的定义域及值域均为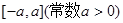 ,其图象如图所示,则方程
,其图象如图所示,则方程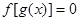 根的个数为 ( )
根的个数为 ( )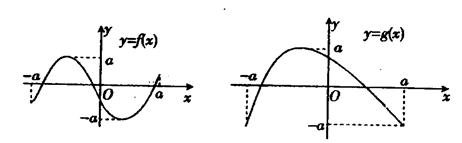
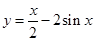 的图象大致是
的图象大致是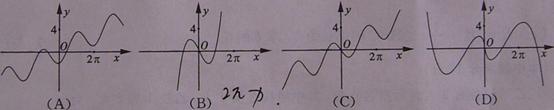
 与函数
与函数 的图像的公共点个数为 .
的图像的公共点个数为 .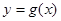 的图像与
的图像与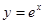 的图像关于直线
的图像关于直线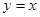 对称,而函数
对称,而函数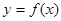 的图像与
的图像与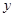 轴对称,若
轴对称,若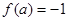 ,则
,则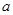 的值是( )
的值是( )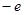



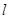 和圆
和圆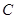 ,当
,当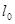 开始在平面上绕端点
开始在平面上绕端点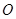 按逆时针方向匀速转动(转动角度不超过
按逆时针方向匀速转动(转动角度不超过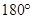 )时,它扫过的圆内阴影部分的面积
)时,它扫过的圆内阴影部分的面积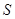 是时间
是时间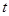 的函数,这个函数的图象大致是( ▲ )
的函数,这个函数的图象大致是( ▲ )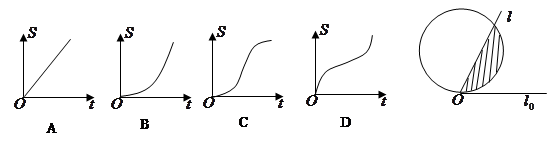
 的图象如上右图所示。
的图象如上右图所示。
 与
与 的图象关于
的图象关于 轴对称,则满足
轴对称,则满足 的实数
的实数 范围是
范围是