题目内容
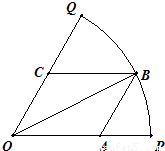
 如图,已知扇形OPQ半径为1,圆心角为
如图,已知扇形OPQ半径为1,圆心角为 ,B是弧PQ上的动点,A、C分别在OP、OQ上,四边形OABC是平行四边形.记∠BOP=α,求当角α取何值时,平行四边形OABC的面积最大?并求出最大面积.
,B是弧PQ上的动点,A、C分别在OP、OQ上,四边形OABC是平行四边形.记∠BOP=α,求当角α取何值时,平行四边形OABC的面积最大?并求出最大面积.
 解:过点B作BM⊥OP于M,
解:过点B作BM⊥OP于M,则BM=sinα,OM=cosα,
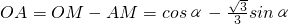 ,…
,…设平行四边形OABC的面积为S,则
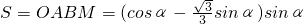 …
…=
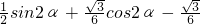 =
=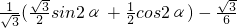 =
=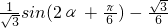 .…
.…由
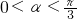 ,得
,得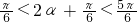 .
.所以当
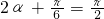 ,即
,即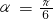 时,
时, .…
.…分析:过点B作BM⊥OP于M,则BM=sinα,OM=cosα,
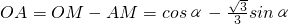 ,从而平行四边形ABOC的面积S=OA•BM,等于
,从而平行四边形ABOC的面积S=OA•BM,等于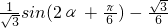 .由0<α<
.由0<α< ,可得当 2α+
,可得当 2α+ =
= 时,S取得最大值.
时,S取得最大值.点评:本题主要考查两角和差的正弦、余弦公式的应用,二倍角公式,正弦函数的定义域和值域,属于中档题.

练习册系列答案
相关题目
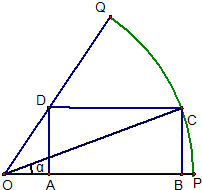 如图,已知OPQ是半径为1,圆心角为
如图,已知OPQ是半径为1,圆心角为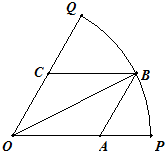 如图,已知扇形OPQ半径为1,圆心角为
如图,已知扇形OPQ半径为1,圆心角为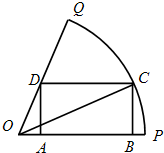 如图,已知OPQ是半径为为1,圆心角为
如图,已知OPQ是半径为为1,圆心角为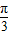 ,B是弧PQ上的动点,A、C分别在OP、OQ上,四边形OABC是平行四边形.记∠BOP=α,求当角α取何值时,平行四边形OABC的面积最大?并求出最大面积.
,B是弧PQ上的动点,A、C分别在OP、OQ上,四边形OABC是平行四边形.记∠BOP=α,求当角α取何值时,平行四边形OABC的面积最大?并求出最大面积.