题目内容
设a为实数,函数 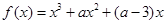 的导函数为
的导函数为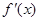 ,且
,且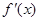 是偶函数,则曲线y=f(x)在原点处的切线方程是________.
是偶函数,则曲线y=f(x)在原点处的切线方程是________.
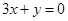
解析试题分析:因为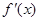 =
=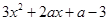 ,由
,由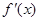 是偶函数知,2a=0,所以
是偶函数知,2a=0,所以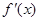 =
=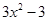 ,所以y=f(x)在原点处的切线斜率为
,所以y=f(x)在原点处的切线斜率为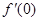 =-3,所以y=f(x)在原点处的切线方程为
=-3,所以y=f(x)在原点处的切线方程为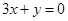 .
.
考点:常见函数的导数,导数的运算法则,函数的奇偶性,函数的切线

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
曲线f(x)=x3+x-2在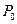 点处的切线平行于直线y=4x-1,则P0点的坐标为 ( )
点处的切线平行于直线y=4x-1,则P0点的坐标为 ( )
| A.(1,0)或(-1,-4) | B.(0,1) | C.(1,0) | D.(-1,-4) |
已知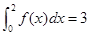 ,则
,则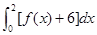 等于 ( )
等于 ( )
| A.9 | B.12 | C.15 | D.18 |
已知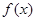 为定义在
为定义在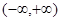 上的可导函数,且
上的可导函数,且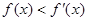 对于
对于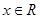 恒成
恒成
立,且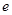 为自然对数的底,则
为自然对数的底,则
A. |
B.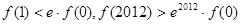 |
C.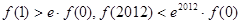 |
D.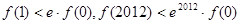 |
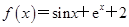 在x=0处的切线方程为________.
在x=0处的切线方程为________.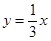 与抛物线
与抛物线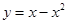 所围图形的面积等于_____________.
所围图形的面积等于_____________.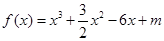 的图象不过第Ⅱ象限,则
的图象不过第Ⅱ象限,则 的取值范围是
的取值范围是 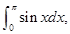 则二项式
则二项式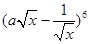 的常数项是 .
的常数项是 .