Question

【题目】给定空间中十个点，其中任意四点不在一个平面上，将某些点之间用线段相连，若得到的图形中没有三角形也没有空间四边形，试确定所连线段数目的最大值.

Answer 1

【答案】15

【解析】

以这十个点为顶点、所连线段为边得一个十阶简单图G.

下面证明：图G的边数不超过15.

设图G的顶点为，共有k条边，用表示顶点的度.

若对均成立，则.

假设存在顶点满足.不妨设，且与均相邻.于是，之间没有边，否则，就形成三角形.从而，之间恰有n条边.

对每个，至多与中的一个顶点相邻（否则，设与 相邻，则就对应了一个空间四边形的四个顶点，这与题设条件矛盾）.从而，与之间的边数至多为

.

在这个顶点之间，由于没有三角形，由托兰定理，知至多有条边.因此，图G的边数为

.

如图所示给出的图共有15条边，且满足要求.

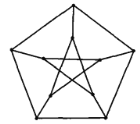
综上，所求边数的最大值为15.