题目内容
17.设A、B是平面上的两个定点,O为坐标原点,P为平面上的点,若$\overrightarrow{OP}$=$\frac{1}{6}$$\overrightarrow{OA}$+$\frac{1}{3}$$\overrightarrow{OB}$,则△AOP与△PAB面积之比为2:3.分析 如图,根据相似比及面积的计算公式可得S△ABO=18S△POC,S△AOP=6S△POC,S△BOP=3S△POC,计算即可.
解答 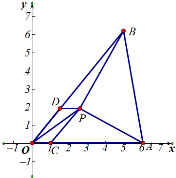 解:如图,过点P作PD∥OA交BO于点D、PC∥BO交OA于点C.
解:如图,过点P作PD∥OA交BO于点D、PC∥BO交OA于点C.
则根据题意、相似比及三角形面积计算公式,
有S△ABO=6×3S△POC=18S△POC,
S△AOP=6S△POC,
S△BOP=3S△POD=3S△POC,
故$\frac{{S}_{△AOP}}{{S}_{△PAB}}=\frac{{S}_{△AOP}}{{S}_{△ABO}-{S}_{△AOP}-{S}_{△BOP}}$
=$\frac{6{S}_{△POC}}{18{S}_{△POC}-6{S}_{△POC}-3{S}_{△POC}}$
=$\frac{2}{3}$
故答案为:2:3.
点评 本题考查向量的平行四边形法则相似比,及同底同高的三角形面积相等,属中档题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
3.某篮球运动员投篮命中的概率为0.7,则他在一次投篮中命中的次数ξ的分布列为( )
| A. |
| B. |
| C. |
| D. |
|
9.曲线y=x(3lnx+1)在点(1,1)处的切线方程为( )
| A. | 4x-3y-1=0 | B. | 3x-2y-1=0 | C. | 4x-y-3=0 | D. | x-y=0 |
 在三棱锥S-ABC中,平面SAB⊥平面SBC,BC⊥SA,AS=AB,过A作AP⊥SB,垂足为F,点E、G分别是棱SA,SC的中点
在三棱锥S-ABC中,平面SAB⊥平面SBC,BC⊥SA,AS=AB,过A作AP⊥SB,垂足为F,点E、G分别是棱SA,SC的中点 已知某几何体的三视图如图所示,其中侧视图是边长为2的正三角形,正视图是矩形,且AA1=3,设D为AA1的中点.
已知某几何体的三视图如图所示,其中侧视图是边长为2的正三角形,正视图是矩形,且AA1=3,设D为AA1的中点.