题目内容
已知椭圆的离心率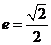 ,左、右焦点分别为
,左、右焦点分别为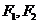 ,定点P
,定点P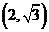 ,点
,点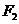 在线段
在线段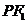 的中垂线上.
的中垂线上.
(1)求椭圆C的方程;
(2)设直线 与椭圆C交于M、N两点,直线
与椭圆C交于M、N两点,直线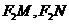 的倾斜角分别为
的倾斜角分别为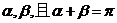 ,求证:直线过定点,并求该定点的坐标.
,求证:直线过定点,并求该定点的坐标.
【答案】
解:⑴由椭圆C的离心率 得
得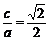 ,其中
,其中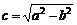 ,
,
椭圆C的左、右焦点分别为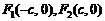 又点
又点 在线段
在线段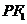 的中垂线上
的中垂线上
∴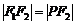 ,∴
,∴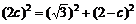 解得c=1,a2=2,b2=1,
解得c=1,a2=2,b2=1,
∴椭圆的方程为 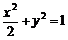 .
.
⑵由题意,知直线MN存在斜率,设其方程为y=kx+m
由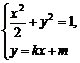 消去y,得(
消去y,得(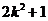 )
)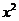 +4kmx+
+4kmx+ =0.
=0.
设M(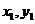 ),N(
),N(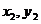 ),则
),则 ,
,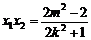
且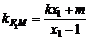 ,
,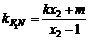
由已知α+β=π,得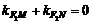 ,即
,即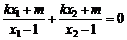
化简,得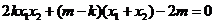
∴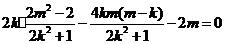 。整理得m=-2k.
。整理得m=-2k.

练习册系列答案
相关题目
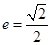 ,左、右焦点分别为
,左、右焦点分别为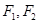 ,定点P
,定点P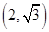 ,点
,点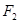 在线段
在线段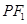 的中垂线上.
的中垂线上.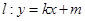 与椭圆C交于M、N两点,直线
与椭圆C交于M、N两点,直线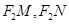 的倾斜角分别为
的倾斜角分别为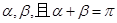 ,求证:直线
,求证:直线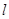 过定点,并求该定点的坐标.
过定点,并求该定点的坐标.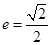 ,左、右焦点分别为
,左、右焦点分别为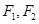 ,定点P
,定点P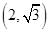 ,点
,点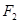 在线段
在线段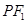 的中垂线上.
的中垂线上.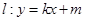 与椭圆C交于M、N两点,直线
与椭圆C交于M、N两点,直线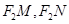 的倾斜角分别为
的倾斜角分别为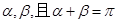 ,求证:直线
,求证:直线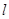 过定点,并求该定点的坐标.
过定点,并求该定点的坐标.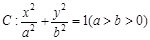 的离心率
的离心率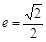 ,左、右焦点分别为F1、F2,
,左、右焦点分别为F1、F2,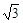 ),点F2在线段PF1的中垂线上.
),点F2在线段PF1的中垂线上.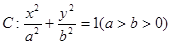 的离心率
的离心率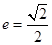 ,左、右焦点分别为F1、F2,点
,左、右焦点分别为F1、F2,点 ,点F2在线段PF1的中垂线上。
,点F2在线段PF1的中垂线上。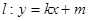 与椭圆C交于M、N两点,直线
与椭圆C交于M、N两点,直线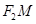 与F2N的倾斜角分别为
与F2N的倾斜角分别为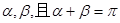 ,试问直线l是否过定点?若过,求该定点的坐标。
,试问直线l是否过定点?若过,求该定点的坐标。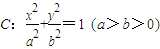 的离心率
的离心率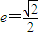 ,左、右焦点分别为F1、F2,点
,左、右焦点分别为F1、F2,点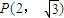 满足F2在线段PF1的中垂线上.
满足F2在线段PF1的中垂线上.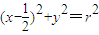 被椭圆C所覆盖,求圆的半径r的最大值.
被椭圆C所覆盖,求圆的半径r的最大值.