Question

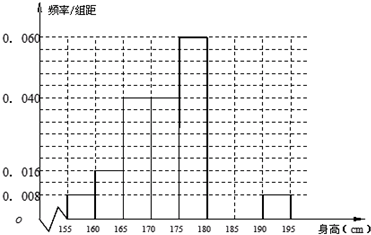
从某学校高三级共1000名男生中随机抽取100名样本测量身高．据测量，被测学生身高全部介于155cm和195cm之间，将测量结果按如下方式分成八组：第一组[155，160），第二组[160，165），…第八组[190，195]．下图是按上述分组方法得到的频率分布直方图的一部分．
（Ⅰ）估计这所学校高三级全体男生身高在165cm以下（不含165cm）的人数；
（Ⅱ）在这100名样本中，已知第六组、第七组、第八组人数依次构成等差数列．求频率分布直方图中第六组的小矩形的高．

Answer 1

分析：（I）根据已知中的频率分布直方图，我们分别求出165cm以上各组矩形的高度和，乘以组距即可得到高在165cm以下（不含165cm）的频率，再乘以样本容量即可得到高在165cm以下（不含165cm）的人数；
（Ⅱ）先求出其他各组的频率，进而得到第六组、第七组的频率，从而计算出其人数，进而得到结论．

解答：解：（Ⅰ）第一组、第八组的频率为P₁=P₈=0.008×5=0.04…（3分）
第二组的频率P₂=0.016×5=0.08…（6分）
∴可估计这所学校高三级全体男生身高在165 cm以下（不含165cm）的人数为：
1000（0.04+0.08）=120人…（7分）
（Ⅱ）第三组、第四组、第五组频率分别为P₃=P₄=0.04×5=0.2，P₅=0.06×5=0.3
∴第六组与第七组的频率和为：1-（P₁+P₂+P₃+P₄+P₅+P₈）=0.14．
∴100名样本中，第六组与第七组人数的和为0.14×100=14，
第八组0.04×100=4…（9分）
设第六组，第七组的人数分别为A₆，A₇，
则2A₇=A₆+4
又A₆+A₇=14
∴A₆=8⇒P₆=

8

100

=0.08；
∴与第二组等高，分布直方图中第六组的小矩形的高为：0.016…（14分）

点评：本题考查的知识点是频率分布直方图，用样本的频率分布估计总体分布，其中频率=矩形的高×组距=频数÷样本容量，是解答本题的关键．