题目内容
从某学校高三年级共1000名男生中随机抽取50人测量身高.据测量,被测学生身高全部介于155cm到195cm之间,将测量结果按如下方式分成八组,第一组[155,160),第二组[160,165),…,第八组[190,195].如图是按上述分组方法得到的频率分布直方图的一部分、其中第六组、第七组、第八组人数依次构成等差数列.
(1)求第六组、第七组的频率,并估算高三年级全体男生身高在180cm以上(含180cm)的人数;
(2)学校决定让这50人在运动会上组成一个高旗队,在这50人中要选身高在180cm以上(含180cm)的三人作为队长,记X为身高在[180,185)的人数,求X的分布列和数学期望.

(1)求第六组、第七组的频率,并估算高三年级全体男生身高在180cm以上(含180cm)的人数;
(2)学校决定让这50人在运动会上组成一个高旗队,在这50人中要选身高在180cm以上(含180cm)的三人作为队长,记X为身高在[180,185)的人数,求X的分布列和数学期望.

分析:(1)由频率分布直方图分析可得后三组的频率,再根据公式:频率=频数÷数据总和,计算可得答案.
(2)列出X的分布列,根据分布列利用随机变量的期望公式求出X的数学期望.
(2)列出X的分布列,根据分布列利用随机变量的期望公式求出X的数学期望.
解答: 解:(1)由频率分布直方图知,前五组频率为(0.008+0.016+0.04+0.04+0.06)×5=0.82,
解:(1)由频率分布直方图知,前五组频率为(0.008+0.016+0.04+0.04+0.06)×5=0.82,
后三组频率为1-0.82=0.18,人数为0.18×50=9人,
这所学校高三男生身高在180cm以上(含180cm)的人数为1000×0.18=180人(4分)
由频率分布直方图得第八组频率为0.008×5=0.04,人数为0.04×50=2人,
设第六组人数为m,则第七组人数为9-2-m=7-m,又m+2=2(7-m),所以m=4,
即第六组人数为4人,第七组人数为3人,
频率分别为0.08,0.06.估算高三年级全体男生身高在180cm以上(含180cm)的人数为180.
(2)X可能的取值为0,1,2,3,
P(x=0)=
=
,P(x=1)=
=
,
P(x=0)=
=
,P(x=0)=
=
,
所以X的分布列
…(10分)
EX=
…(12分)
 解:(1)由频率分布直方图知,前五组频率为(0.008+0.016+0.04+0.04+0.06)×5=0.82,
解:(1)由频率分布直方图知,前五组频率为(0.008+0.016+0.04+0.04+0.06)×5=0.82,后三组频率为1-0.82=0.18,人数为0.18×50=9人,
这所学校高三男生身高在180cm以上(含180cm)的人数为1000×0.18=180人(4分)
由频率分布直方图得第八组频率为0.008×5=0.04,人数为0.04×50=2人,
设第六组人数为m,则第七组人数为9-2-m=7-m,又m+2=2(7-m),所以m=4,
即第六组人数为4人,第七组人数为3人,
频率分别为0.08,0.06.估算高三年级全体男生身高在180cm以上(含180cm)的人数为180.
(2)X可能的取值为0,1,2,3,
P(x=0)=
| ||
|
| 5 |
| 42 |
| ||||
|
| 20 |
| 42 |
P(x=0)=
| ||||
|
| 15 |
| 42 |
| ||
|
| 2 |
| 42 |
所以X的分布列
| X | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
EX=
| 4 |
| 3 |
点评:本题是对频率、频数灵活运用的综合考查,各小组频数之和等于数据总和,各小组频率之和等于1.频率、频数的关系:频率=频数÷数据总和,同时还考查了古典概型的计算和离散型随机变量的期望与方差.

练习册系列答案
相关题目
 从某学校高三年级共800名男生中随机抽取50名测量身高,测量发现被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160)、第二组[160,165);…第八组[190,195],右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.
从某学校高三年级共800名男生中随机抽取50名测量身高,测量发现被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160)、第二组[160,165);…第八组[190,195],右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.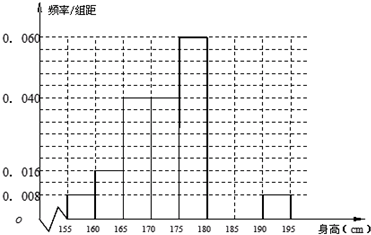
 (2012•咸阳三模)从某学校高三年级共800名男生中随机抽取50人测量身高. 据测量,被测学生身高全部介于155cm到195cm之间,将测量结果按如下方式分成八组:第一组[155,160);第二组[160,165);…;第八组[190,195).
(2012•咸阳三模)从某学校高三年级共800名男生中随机抽取50人测量身高. 据测量,被测学生身高全部介于155cm到195cm之间,将测量结果按如下方式分成八组:第一组[155,160);第二组[160,165);…;第八组[190,195). 从某学校高三年级共800名男生中随机抽取50名测量身高,据测量被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组;第一组[155,160)、第二组[160,165);…第八组[190,195),如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.
从某学校高三年级共800名男生中随机抽取50名测量身高,据测量被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组;第一组[155,160)、第二组[160,165);…第八组[190,195),如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.