题目内容
(本小题满分12分) 若曲线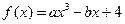 在
在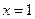 处的切线方程
处的切线方程
为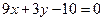 .
.
(1)求函数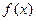 的解析式;
的解析式;
(2)(理)若方程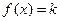 有3个实数解,求实数
有3个实数解,求实数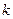 的取值范围.
的取值范围.
(文)求函数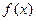 的单调区间
的单调区间
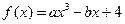 在
在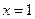 处的切线方程
处的切线方程为
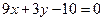 .
.(1)求函数
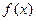 的解析式;
的解析式;(2)(理)若方程
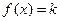 有3个实数解,求实数
有3个实数解,求实数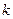 的取值范围.
的取值范围. (文)求函数
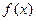 的单调区间
的单调区间(1)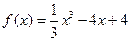 ;
;
(2)(理)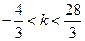 ;
;
(文)函数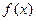 的单调递增区间为
的单调递增区间为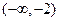 ,
,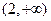 ;单调递减区间为
;单调递减区间为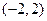 。
。
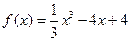 ;
;(2)(理)
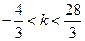 ;
;(文)函数
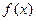 的单调递增区间为
的单调递增区间为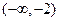 ,
,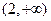 ;单调递减区间为
;单调递减区间为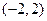 。
。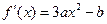 …………………1分
…………………1分(1)
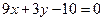 的斜率为-3,切点为
的斜率为-3,切点为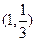 ……………….3分
……………….3分∴
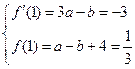 解得
解得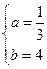 ………………………5分
………………………5分∴所求解析式为
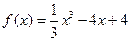 ……………………6分
……………………6分(2)由(1)得
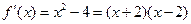 ,令
,令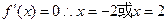 …….7分
…….7分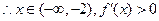 ,函数
,函数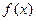 是增函数
是增函数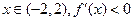 ,函数
,函数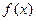 是减函数
是减函数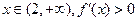 ,函数
,函数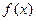 是增函数……………(理9分) (文10分)
是增函数……………(理9分) (文10分)(文:∴函数
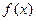 的单调递增区间为:
的单调递增区间为: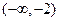 ,
,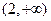
单调递减区间为:
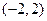 …………….(文)12分)
…………….(文)12分)理:因此:当
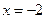 时,
时,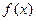 有极大值
有极大值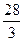 ,当
,当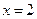 时,
时,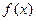 有极小值
有极小值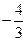
…………..11分
且
 ,
,∴由
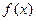 的图像可知
的图像可知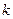 的取值范围为
的取值范围为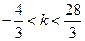 …………….12分
…………….12分
练习册系列答案
相关题目
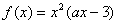 ,其中a为常数。
,其中a为常数。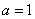 ,求:
,求: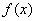 的图象在点
的图象在点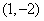 处的切线方程;
处的切线方程;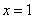 是函数
是函数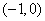 上是增函数,求:实数a的取值范围。
上是增函数,求:实数a的取值范围。 在点
在点 处的切线方程是
处的切线方程是 ,则( )
,则( ) B
B  C
C 
 D
D 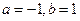
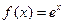 ②
②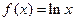 ③
③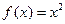 ④
④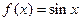
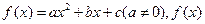 的导函数是
的导函数是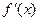 ,集合
,集合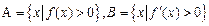 ,若
,若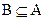 ,则 ( )
,则 ( )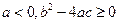
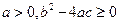
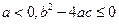
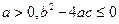
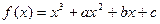 作代换
作代换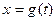 ,则总不会改变
,则总不会改变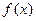 的值域的代换是
的值域的代换是
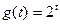
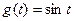

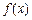 为可导函数,
为可导函数,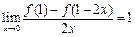 ,则在点(1,
,则在点(1,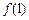 )处的切线斜率为( )
)处的切线斜率为( )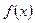 =
=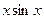 ,若
,若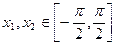 ,且
,且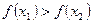 ,则下列不等式必定成立的是
,则下列不等式必定成立的是



 在点
在点 处的切线方程为( )
处的切线方程为( ) B
B  C
C  D
D 