题目内容
如图所示,在边长为12的正方形ADD1A1中,点B,C在线段AD上,且AB=3,BC=4,作BB1∥AA1,分别交A1D1,AD1于点B1,P,作CC1∥AA1,分别交A1D1,AD1于点C1,Q,将该正方形沿BB1,CC1折叠,使得DD1与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1.
(Ⅰ)求证:AB⊥平面BCC1B1;
(Ⅱ)求四棱锥A-BCQP的体积。
(Ⅰ)求证:AB⊥平面BCC1B1;
(Ⅱ)求四棱锥A-BCQP的体积。
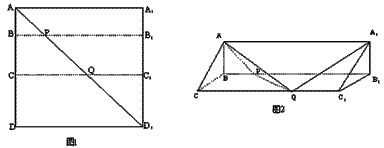
(Ⅰ)证明:在正方形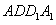 中,因为CD=AD-AB-BC=5,
中,因为CD=AD-AB-BC=5,
 的底面三角形ABC的边AC=5,
的底面三角形ABC的边AC=5,
因为AB=3,BC=4,所以,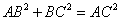 ,所以,AB⊥BC,
,所以,AB⊥BC,
因为四边形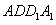 为正方形,
为正方形,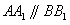 ,
,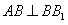 ,
,
而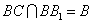 ,
,
所以,AB⊥平面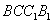 .
.
(Ⅱ)解:因为AB⊥平面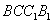 ,
,
所以,AB为四棱锥A-BCQP的高,
因为四边形BCQP为直角梯形,且BP=AB=3,CQ=AB+BC=7,
所以,梯形BCQP的面积为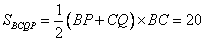 ,
,
所以,四棱锥A-BCQP的体积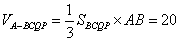 。
。
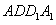 中,因为CD=AD-AB-BC=5,
中,因为CD=AD-AB-BC=5, 的底面三角形ABC的边AC=5,
的底面三角形ABC的边AC=5,因为AB=3,BC=4,所以,
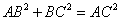 ,所以,AB⊥BC,
,所以,AB⊥BC,因为四边形
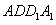 为正方形,
为正方形,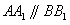 ,
,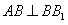 ,
,而
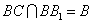 ,
,所以,AB⊥平面
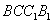 .
.(Ⅱ)解:因为AB⊥平面
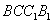 ,
,所以,AB为四棱锥A-BCQP的高,
因为四边形BCQP为直角梯形,且BP=AB=3,CQ=AB+BC=7,
所以,梯形BCQP的面积为
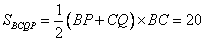 ,
,所以,四棱锥A-BCQP的体积
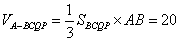 。
。
练习册系列答案
相关题目
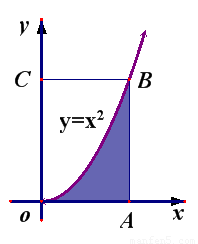
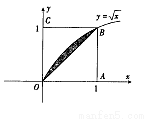
 (2012•福建)如图所示,在边长为1的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为( )
(2012•福建)如图所示,在边长为1的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为( )
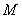

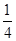 B、
B、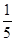 C、
C、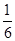 D、
D、