题目内容
下列四个命题:①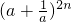 的常数项是第n项;②(a+b)2n的前n项二项式系数之和等于后n项二项式系数之和,均等于22n-1;③
的常数项是第n项;②(a+b)2n的前n项二项式系数之和等于后n项二项式系数之和,均等于22n-1;③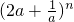 展开式中a的正指数项的系数之和大于a的负指数项的系数之和;④(3x+28x2-1)99•(5x-7x2+2)8的常数项是28其中正确命题的个数为
展开式中a的正指数项的系数之和大于a的负指数项的系数之和;④(3x+28x2-1)99•(5x-7x2+2)8的常数项是28其中正确命题的个数为
- A.1
- B.2
- C.3
- D.4
A
分析:①根据二项式展开式的通项可得当r=n时即Tr+1是常数项.②展开式共有2n+1项,并且所有项的二项式系数之和22n.
③a正指数项的系数之和为Cn02n+Cn12n-1+Cn22n-2+…,a的负指数项的系数之和为Cnn20+Cnn-121+Cnn-222+….
④常数项是-28.
解答:①由题意可得: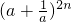 展开式的通项为Tr+1=C2nra2n-2r,所以当r=n时即Tr+1是常数项,所以①错误.
展开式的通项为Tr+1=C2nra2n-2r,所以当r=n时即Tr+1是常数项,所以①错误.
②由题意可得:(a+b)2n的展开式共有2n+1项,并且所有项的二项式系数之和22n,所以展开式的前n项二项式系数之和与后n项二项式系数之和均等于22n-1错误,所以②错误.
③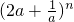 展开式的通项为Tr+1=2n-rCnran-2r,a正指数项的系数之和为Cn02n+Cn12n-1+Cn22n-2+…,a的负指数项的系数之和为Cnn20+Cnn-121+Cnn-222+…,所以③正确.
展开式的通项为Tr+1=2n-rCnran-2r,a正指数项的系数之和为Cn02n+Cn12n-1+Cn22n-2+…,a的负指数项的系数之和为Cnn20+Cnn-121+Cnn-222+…,所以③正确.
④(3x+28x2-1)99•(5x-7x2+2)8=[(3x+28x2)-1]99•[(5x-7x2)+2]8的常数项是-28,所以④错误.
故选A.
点评:本题主要考查二项式定理的应用,以及二项展开式的有关性质与通项.
分析:①根据二项式展开式的通项可得当r=n时即Tr+1是常数项.②展开式共有2n+1项,并且所有项的二项式系数之和22n.
③a正指数项的系数之和为Cn02n+Cn12n-1+Cn22n-2+…,a的负指数项的系数之和为Cnn20+Cnn-121+Cnn-222+….
④常数项是-28.
解答:①由题意可得:
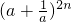 展开式的通项为Tr+1=C2nra2n-2r,所以当r=n时即Tr+1是常数项,所以①错误.
展开式的通项为Tr+1=C2nra2n-2r,所以当r=n时即Tr+1是常数项,所以①错误.②由题意可得:(a+b)2n的展开式共有2n+1项,并且所有项的二项式系数之和22n,所以展开式的前n项二项式系数之和与后n项二项式系数之和均等于22n-1错误,所以②错误.
③
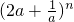 展开式的通项为Tr+1=2n-rCnran-2r,a正指数项的系数之和为Cn02n+Cn12n-1+Cn22n-2+…,a的负指数项的系数之和为Cnn20+Cnn-121+Cnn-222+…,所以③正确.
展开式的通项为Tr+1=2n-rCnran-2r,a正指数项的系数之和为Cn02n+Cn12n-1+Cn22n-2+…,a的负指数项的系数之和为Cnn20+Cnn-121+Cnn-222+…,所以③正确.④(3x+28x2-1)99•(5x-7x2+2)8=[(3x+28x2)-1]99•[(5x-7x2)+2]8的常数项是-28,所以④错误.
故选A.
点评:本题主要考查二项式定理的应用,以及二项展开式的有关性质与通项.

练习册系列答案
相关题目