题目内容
定义:对于映射f:A→B,如果A中的不同元素有不同的象,且B中的每一个元素都有原象,则称f:A→B为一一映射.如果存在对应关系φ,使A到B成为一一映射,则称A和B具有相同的势.给出下列命题:①A={奇数},B={偶数},则A和B 具有相同的势;
②A是直角坐标系平面内所有点形成的集合,B是复数集,则A和B 不具有相同的势;
③若A={
 ,
,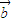 },其中
},其中 ,
, 是不共线向量,B={
是不共线向量,B={ |
| 与
与 ,
, 共面的任意向量},则A和B不可能具有相同的势;
共面的任意向量},则A和B不可能具有相同的势;④若区间A=(-1,1),B=(-∞,+∞),则A和B具有相同的势.
其中真命题为 .
【答案】分析:根据奇数与偶数的定义,给出一个对应法则可验证①的正确性;
对②,根据复数的几何意义,可判断能否形成一一映射,来判断②是否正确;
根据平面向量定理可判断③是否正确;
对④,给出对应法则y=tan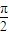 x,可验证④的正确性.
x,可验证④的正确性.
解答:解:根据一一映射的定义,集合A={奇数}→B={偶数},不妨给出对应法则加1.则A→B是一一映射,故①正确;
对②设Z点的坐标(a,b),则Z点对应复数a+bi,a、b∈R,复合一一映射的定义,故②不正确;
对③∵A中的不同元素可以有相同的象,∴A和B不具有相同的势,故③正确;
对④,给出对应法则y=tan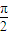 x,对于A,B两集合可形成f:A→B的一一映射,则A、B具有相同的势;∴④正确.
x,对于A,B两集合可形成f:A→B的一一映射,则A、B具有相同的势;∴④正确.
故答案是①③④
点评:本题借助考查命题的真假判断,考查一一映射的定义.
对②,根据复数的几何意义,可判断能否形成一一映射,来判断②是否正确;
根据平面向量定理可判断③是否正确;
对④,给出对应法则y=tan
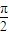 x,可验证④的正确性.
x,可验证④的正确性.解答:解:根据一一映射的定义,集合A={奇数}→B={偶数},不妨给出对应法则加1.则A→B是一一映射,故①正确;
对②设Z点的坐标(a,b),则Z点对应复数a+bi,a、b∈R,复合一一映射的定义,故②不正确;
对③∵A中的不同元素可以有相同的象,∴A和B不具有相同的势,故③正确;
对④,给出对应法则y=tan
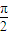 x,对于A,B两集合可形成f:A→B的一一映射,则A、B具有相同的势;∴④正确.
x,对于A,B两集合可形成f:A→B的一一映射,则A、B具有相同的势;∴④正确.故答案是①③④
点评:本题借助考查命题的真假判断,考查一一映射的定义.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目