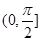题目内容
给出下列命题,其中正确的命题是 (写出所有正确命题的编号).①在△ABC中,若tanA+tanB+tanC>0,则△ABC是锐角三角形;
②在△ABC中,A<B是cosA>cosB的充要条件;
③已知非零向量
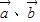 ,则“
,则“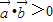 ”是“
”是“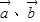 的夹角为锐角”的充要条件;
的夹角为锐角”的充要条件;④若数列{an}为等比数列,则“a3a5=16”是“a4=4”的充分不必要条件;
⑤函数f(x)的导函数为f'(x),若对于定义域内任意x1,x2(x1≠x2),有
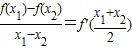 恒成立,则称f(x)为恒均变函数,那么f(x)=x2-2x+3为恒均变函数.
恒成立,则称f(x)为恒均变函数,那么f(x)=x2-2x+3为恒均变函数.
【答案】分析:①依据正切和角公式的变形及诱导公式推导;
②由于A、B是三角形的内角,得到A,B∈(0,π),在(0,π)上,y=cosx是减函数.
由此知△ABC中,“A>B”?“cosA<cosB”,即可得答案;
③夹角为0°时,也可使则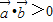 ;
;
④依据等比数列的性质;
⑤对于所给的每一个函数,分别计算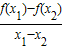 和
和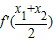 的值,检验二者是否相等,从而根据恒均变函数”的定义,做出判断.
的值,检验二者是否相等,从而根据恒均变函数”的定义,做出判断.
解答:解:①根据正切和角公式tan(A+B)=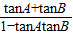 得到,
得到,
tanA+tanB=-tanC+tanAtanBtanC,
又tan(A+B)=tan(180°-C)=-tanC,
∴tanA+tanB+tanC=tanA•tanB•tanC,
若三角形有一个为钝角,必有一个值为负值,tanA•tanB•tanC<0,
若三角形有一个为直角,则tanA•tanB•tanC无意义,若∠C=90度,tanC无意义,
当tanA•tanB•tanC>0时三个角为锐角,
故tanA+tanB+tanC>0时,为锐角三角形,故①正确;
②∵A、B是三角形的内角,∴A∈(0,π),B∈(0,π),
∵在(0,π)上,y=cosx是减函数,
∴△ABC中,“A>B”?“cosA<cosB”,故②正确;
③非零向量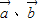 ,∵
,∵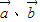 的夹角为锐角,∴
的夹角为锐角,∴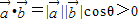 ,
,
∵当夹角θ=0°时,满足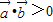 ,故③错;
,故③错;
④∵数列{an}为等比数列,∴若a3a5=16,则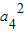 =16,即a4=±4,故④错;
=16,即a4=±4,故④错;
⑤∵f(x)=x2-2x+3,
∴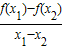 =
=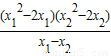 =
=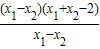 =x1+x2-2,
=x1+x2-2,
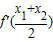 =2•
=2•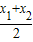 -2=x1+x2-2,
-2=x1+x2-2,
故满足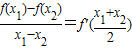 ,∴f(x)=x2-2x+3,为恒均变函数.
,∴f(x)=x2-2x+3,为恒均变函数.
点评:本题主要考查判断命题的真假,属于基础题,同时考查函数的导数运算,条件的判断及正切和角公式.
②由于A、B是三角形的内角,得到A,B∈(0,π),在(0,π)上,y=cosx是减函数.
由此知△ABC中,“A>B”?“cosA<cosB”,即可得答案;
③夹角为0°时,也可使则
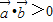 ;
;④依据等比数列的性质;
⑤对于所给的每一个函数,分别计算
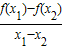 和
和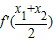 的值,检验二者是否相等,从而根据恒均变函数”的定义,做出判断.
的值,检验二者是否相等,从而根据恒均变函数”的定义,做出判断.解答:解:①根据正切和角公式tan(A+B)=
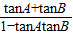 得到,
得到,tanA+tanB=-tanC+tanAtanBtanC,
又tan(A+B)=tan(180°-C)=-tanC,
∴tanA+tanB+tanC=tanA•tanB•tanC,
若三角形有一个为钝角,必有一个值为负值,tanA•tanB•tanC<0,
若三角形有一个为直角,则tanA•tanB•tanC无意义,若∠C=90度,tanC无意义,
当tanA•tanB•tanC>0时三个角为锐角,
故tanA+tanB+tanC>0时,为锐角三角形,故①正确;
②∵A、B是三角形的内角,∴A∈(0,π),B∈(0,π),
∵在(0,π)上,y=cosx是减函数,
∴△ABC中,“A>B”?“cosA<cosB”,故②正确;
③非零向量
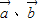 ,∵
,∵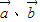 的夹角为锐角,∴
的夹角为锐角,∴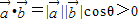 ,
,∵当夹角θ=0°时,满足
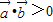 ,故③错;
,故③错;④∵数列{an}为等比数列,∴若a3a5=16,则
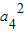 =16,即a4=±4,故④错;
=16,即a4=±4,故④错;⑤∵f(x)=x2-2x+3,
∴
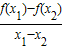 =
=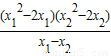 =
=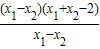 =x1+x2-2,
=x1+x2-2,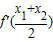 =2•
=2•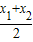 -2=x1+x2-2,
-2=x1+x2-2,故满足
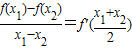 ,∴f(x)=x2-2x+3,为恒均变函数.
,∴f(x)=x2-2x+3,为恒均变函数.点评:本题主要考查判断命题的真假,属于基础题,同时考查函数的导数运算,条件的判断及正切和角公式.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 如图,边长为a的正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,现给出下列命题,其中正确的命题有
如图,边长为a的正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,现给出下列命题,其中正确的命题有

 线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,现给出下列命题,其中正确的命题有 (只需填上正确命题的序号).
线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,现给出下列命题,其中正确的命题有 (只需填上正确命题的序号). .
.
 线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,现给出下列命题,其中正确的命题有
(只需填上正确命题的序号).
线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,现给出下列命题,其中正确的命题有
(只需填上正确命题的序号). .
.