题目内容
设f(x)=x2+px+q,A={x|x=f(x)},B={x|f[f(x)]=x}.

(1)求证:A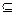 B;
B;
(2)如果A={-1,3},求B。

(1)求证:A
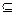 B;
B;(2)如果A={-1,3},求B。
(1)证明略(2) B={-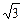 ,-1,
,-1,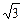 ,3}
,3}
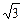 ,-1,
,-1,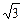 ,3}
,3}(1)证明: 设x0是集合A中的任一元素,即有x0∈A.
∵A={x|x=f(x)},∴x0=f(x0).
即有f[f(x0)]=f(x0)=x0,∴x0∈B,故A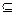 B.
B.
(2)证明:∵A={-1,3}={x|x2+px+q=x},
∴方程x2+(p-1)x+q=0有两根-1和3,应用韦达定理,得
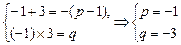
∴f(x)=x2-x-3.
于是集合B的元素是方程f[f(x)]=x,
也即(x2-x-3)2-(x2-x-3)-3=x (*) 的根.
将方程(*)变形,得(x2-x-3)2-x2=0
解得x=1,3,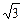 ,-
,-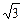 .
.
故B={-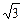 ,-1,
,-1,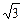 ,3}.
,3}.
∵A={x|x=f(x)},∴x0=f(x0).
即有f[f(x0)]=f(x0)=x0,∴x0∈B,故A
 B.
B.(2)证明:∵A={-1,3}={x|x2+px+q=x},
∴方程x2+(p-1)x+q=0有两根-1和3,应用韦达定理,得
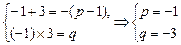
∴f(x)=x2-x-3.
于是集合B的元素是方程f[f(x)]=x,
也即(x2-x-3)2-(x2-x-3)-3=x (*) 的根.
将方程(*)变形,得(x2-x-3)2-x2=0
解得x=1,3,
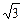 ,-
,-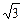 .
.故B={-
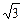 ,-1,
,-1,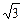 ,3}.
,3}.
练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目

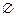 和A∩C=
和A∩C=
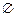 ,证明此结论.
,证明此结论. 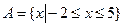 ,
,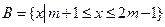 ,
,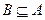 ,求
,求 的取值范围。
的取值范围。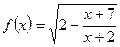 的定义域为
的定义域为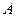 ,
,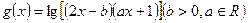 的定义域为
的定义域为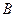 。
。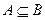 ,求
,求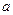 、
、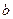 的取值范围。
的取值范围。 ,则下列命题中正确命题的序号有 . (请将你认为正确命题的序号都填上)
,则下列命题中正确命题的序号有 . (请将你认为正确命题的序号都填上) 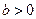 时,函数
时,函数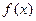 在R上是单调增函数;
在R上是单调增函数; 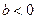 时,函数
时,函数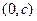 对称;
对称; 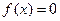 可能有三个实数根.
可能有三个实数根. 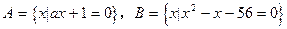 ,
, 若
若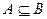 ,则由实数a组成的集合C为 。
,则由实数a组成的集合C为 。