题目内容
已知函数f(x)=loga[(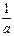 -2)x+1]在区间[1,2]上恒为正,求实数a的取值范围.
-2)x+1]在区间[1,2]上恒为正,求实数a的取值范围.
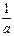 -2)x+1]在区间[1,2]上恒为正,求实数a的取值范围.
-2)x+1]在区间[1,2]上恒为正,求实数a的取值范围.解:∵f(x)=loga[(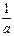 -2)x+1]在[1,2]上恒正,……………………2分
-2)x+1]在[1,2]上恒正,……………………2分
(1)当 a>1
a>1 时,真数μ=(
时,真数μ=(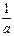 -2)x+1>1,
-2)x+1>1,
∴(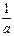 -2)x>0,∴
-2)x>0,∴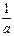 -2>0即a<
-2>0即a<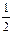 (舍) .………………………………6分
(舍) .………………………………6分
(2)当0<a<1时,0<μ<1
∴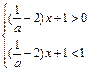
要使①式当x∈[1,2]恒成立,则
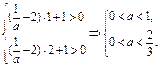 ∴0<a<
∴0<a<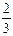 .
.
要使②式成立,则(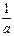 -2)x<0,只要
-2)x<0,只要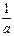 -2<0,∴
-2<0,∴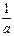 <2 ,∴a>
<2 ,∴a>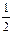 .
.
综上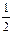 <a<
<a<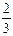 .………………………………12分
.………………………………12分
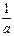 -2)x+1]在[1,2]上恒正,……………………2分
-2)x+1]在[1,2]上恒正,……………………2分(1)当
 a>1
a>1 时,真数μ=(
时,真数μ=(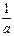 -2)x+1>1,
-2)x+1>1,∴(
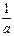 -2)x>0,∴
-2)x>0,∴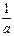 -2>0即a<
-2>0即a<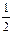 (舍) .………………………………6分
(舍) .………………………………6分(2)当0<a<1时,0<μ<1
|
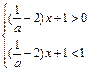
要使①式当x∈[1,2]恒成立,则
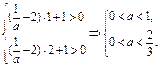 ∴0<a<
∴0<a<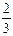 .
.要使②式成立,则(
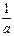 -2)x<0,只要
-2)x<0,只要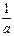 -2<0,∴
-2<0,∴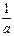 <2 ,∴a>
<2 ,∴a>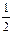 .
.综上
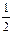 <a<
<a<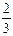 .………………………………12分
.………………………………12分略

练习册系列答案
相关题目
 满足
满足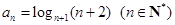 ,若正整数
,若正整数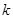 满足
满足 为整数,则称
为整数,则称 内所有的企盼数的和为( )
内所有的企盼数的和为( )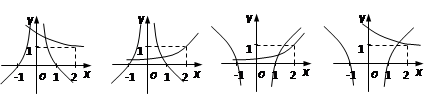
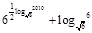
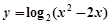 单调递增区间是 ▲ .
单调递增区间是 ▲ . ___________.
___________.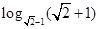 的结果是( )
的结果是( )

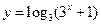 的值域为________________________.
的值域为________________________. 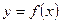 图象与函数
图象与函数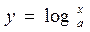 图象关于直线
图象关于直线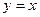 对称,则函数
对称,则函数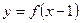 图象过定点:
图象过定点: