题目内容
从某小学随机抽取100名同学，将他们的身高（单位：厘米）数据绘制成频率分布直方图（如图）．若要从身高在[ 120 , 130），[130 ，140） , [140 , 150]三组内的学生中，用分层抽样的方法选取18人参加一项活动，则从身高在[140 ，150]内的学生中选取的人数应为（ ）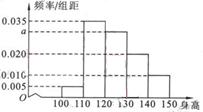
A． | B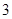． | C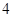． | D． |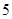
B
解析试题分析：依题意可得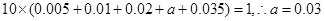
．所以身高在[ 120 , 130），[130 ，140） , [140 , 150]三组内的学生比例为3:2:1．所以从身高在[140 ，150]内的学生中选取的人数应为3．
考点：1．统计的知识．2．分层抽样的方法．3．识别图标的能力．
,
,若低于60分的人数是15人,则该班的学生人数是（ ） 
在某地区某高传染性病毒流行期间，为了建立指标显示疫情已受控制，以便向该地区居众显示可以过正常生活，有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”，根据连续
7天的新增病例数计算，下列各选项中，一定符合上述指标的是（ ）
①平均数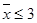
；
②标准差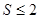
；
③平均数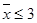且标准差；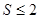
④平均数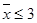且极差小于或等于2；
⑤众数等于1且极差小于或等于1。
| A．①② | B．③④ | C．③④⑤ | D．④⑤ |
某班的全体学生参加英语测试，成绩的频率分布直方图如图，数据的分组依次为：[20,40)，[40,60)，[60,80)，[80,100]．若低于60分的人数是15，则该班的学生人数是( )
| A．45 | B．50 |
| C．55 | D．60 |
[2012·四川高考]交通管理部门为了解机动车驾驶员(简称驾驶员)对某新法规的知晓情况，对甲、乙、丙、丁四个社区做分层抽样调查．假设四个社区驾驶员的总人数为N，其中甲社区有驾驶员96人．若在甲、乙、丙、丁四个社区抽取驾驶员的人数分别为12,21,25,43，则这四个社区驾驶员的总人数N为( )
| A．101 | B．808 | C．1212 | D．2012 |
设
，…，
是变量
和
的
个样本点，直线
是由这些样本点通过最小二乘法得到的线性回归方程（如图），以下结论中正确的是（ ）
| A．和的相关系数为直线的斜率 |
| B．和的相关系数在0到1之间 |
| C．当为偶数时，分布在两侧的样本点的个数一定相同 |
D．直线过点 |
容量为20的样本数据，分组后的频数如下表
| 分组 | [10，20） | [20，30） | [30，40） | [40，50） | [50，60） | [60，70） |
| 频数 | 2 | 3 | 4 | 5 | 4 | 2 |
A．0.35 B．0.45 C．0.55 D．0.65