题目内容
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() .
.
(I)求证:![]() 是等比数列;
是等比数列;
(II)求证:![]() 不是等比数列.
不是等比数列.
【答案】(1) 证明见解析.
(2)证明见解析.
【解析】分析:(I)由![]() ,则
,则![]() 时,
时,![]() ,两式相减,化简得到
,两式相减,化简得到
![]() ,即可得到数理
,即可得到数理![]() 是公比为
是公比为![]() 的等比数列;
的等比数列;
(II)(方法一)由(I)知![]() 是等比数列,所以
是等比数列,所以![]() ,于是
,于是![]() ,解得
,解得![]() ,即可得到数列
,即可得到数列![]() 不是等比数列.
不是等比数列.
(方法二) 由(I)得![]() ,因此
,因此![]() ,求得于是
,求得于是![]() 假设
假设![]() 是等比数列,则有
是等比数列,则有![]() ,解得
,解得![]() ,即可得
,即可得![]() 不是等比数列.
不是等比数列.
详解:(I)因为![]() ,所以当
,所以当![]() 时
时![]() ,
,
两式相减得![]() ,
,
即![]() ,
,
因此![]() ,
,
故![]() 是公比为
是公比为![]() 的等比数列.
的等比数列.
(II)(方法一)假设![]() 是等比数列,则有
是等比数列,则有![]() ,
,
即![]() .
.
由(I)知![]() 是等比数列,所以
是等比数列,所以![]() ,
,
于是![]() ,即
,即![]() ,解得
,解得![]() ,
,
这与![]() 是等比数列相矛盾,
是等比数列相矛盾,
故假设错误,即![]() 不是等比数列.
不是等比数列.
(方法二) 由(I)知![]() ,所以
,所以![]() ,因此
,因此![]() .
.
于是![]() ,
,
假设![]() 是等比数列,则有
是等比数列,则有![]() ,
,
即![]() ,解得
,解得![]() ,
,
这与![]() 相矛盾,
相矛盾,
故假设错误,即![]() 不是等比数列.
不是等比数列.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
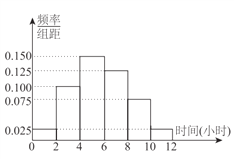
【题目】某中学共有5000人,其中男生3500人,女生1500人,为了了解该校学生每周平均体育锻炼时间的情况以及该校学生每周平均体育锻炼时间是否与性别有关,现在用分层抽样的方法从中收集300位学生每周平均体育锻炼时间的样本数据(单位:小时),其频率分布直方图如下:
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
已知在样本数据中,有60位女生的每周平均体育锻炼时间超过4小时,根据独立性检验原理,我们( )
A. 没有理由认为“该校学生每周平均体育锻炼时间与性别有关”
B. 有![]() 的把握认为“该校学生每周平均体育锻炼时间与性别有关”
的把握认为“该校学生每周平均体育锻炼时间与性别有关”
C. 有![]() 的把握认为“该校学生每周平均体育锻炼时间与性别无关”
的把握认为“该校学生每周平均体育锻炼时间与性别无关”
D. 有![]() 的把握认为“该校学生每周平均体育锻炼时间与性别有关”
的把握认为“该校学生每周平均体育锻炼时间与性别有关”