题目内容
(本题满分12分)
已知定义域为 的函数
的函数 同时满足以下三个条件:
同时满足以下三个条件:
①对任意的 ,总有
,总有 ;②
;② ;③若
;③若 且
且 ,则有
,则有 成立,则称
成立,则称 为“友谊函数”.
为“友谊函数”.
(Ⅰ)若已知 为“友谊函数”,求
为“友谊函数”,求 的值;
的值;
(Ⅱ)函数 在区间
在区间 上是否为“友谊函数”?并给出理由;
上是否为“友谊函数”?并给出理由;
(Ⅲ)已知 为“友谊函数”,且
为“友谊函数”,且
 ,求证:
,求证: .
.
【答案】
(Ⅰ)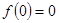
(Ⅱ) 满足条件①﹑②﹑③所以
满足条件①﹑②﹑③所以 为友谊函数
为友谊函数
(Ⅲ)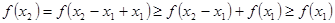
【解析】解:(Ⅰ)取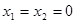 得
得 ,又由
,又由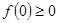 ,得
,得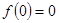 ………………2分
………………2分
(Ⅱ)显然 在
在 上满足①
上满足①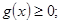 ②
②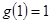 ,若
,若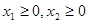 ,且
,且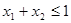 ,则有
,则有 故
故 满足条件①﹑②﹑③所以
满足条件①﹑②﹑③所以 为友谊函数. ………………7分
为友谊函数. ………………7分
(Ⅲ)因为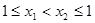 ,则0<
,则0< <1,
<1,
所以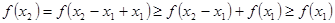 . ………………12分
. ………………12分
|
|||
|

练习册系列答案
相关题目
 <1,xÎR }.
<1,xÎR }. ,求实数a的取值范围.
,求实数a的取值范围. (
( ,
, 为常数),且方程
为常数),且方程 有两个实根为
有两个实根为 .
. 的解析式;
的解析式; 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
, 为
为 上的点,且
上的点,且 ⊥平面
⊥平面
 ⊥平面
⊥平面
 的大小;
的大小; 到平面
到平面