题目内容
-个球的表面积为144π,在该球的球面上有P、Q、R三点,且每两点间的球面距离均为3π,则过P、Q、R三点的截面到球心的距离为( )
A、3
| ||
B、3
| ||
C、2
| ||
D、2
|
分析:先确定内接体的形状,确定球心与平面ABC的关系,然后求解距离.
解答:解:球的表面积为144π,
∴R=6,又每两点间的球面距离均为3π,
∴每两点间的夹角为90°,
显然OA、OB、OC两两垂直,
设O1为ABC所在平面截球所得圆的圆心,
∵OA=OB=OC=6,且OA⊥OB⊥OC,
∴AB=BC=CA=6
.
∴O1为△ABC的中心.∴O1A=2
.
由OO12+O1A2=OA2,可得OO1=2
.
故选D.
∴R=6,又每两点间的球面距离均为3π,
∴每两点间的夹角为90°,
显然OA、OB、OC两两垂直,
设O1为ABC所在平面截球所得圆的圆心,
∵OA=OB=OC=6,且OA⊥OB⊥OC,
∴AB=BC=CA=6
| 2 |
∴O1为△ABC的中心.∴O1A=2
| 6 |
由OO12+O1A2=OA2,可得OO1=2
| 3 |
故选D.
点评:本题考查球的内接体问题,球心与平面的距离关系,考查空间想象能力,是中档题.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
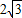 ,BD=
,BD=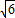 ,则该球的表面积为( )
,则该球的表面积为( )