题目内容
已知定义在(－1，1)上的函数f(x)满足f
＝1，且对x、y∈(－1，1)时，有f(x)－f(y)＝
．
(1)判断f(x)在(－1，1)上的奇偶性，并证明之；
(2)令x1＝
，xn+1＝
，求数列{f(xn)}的通项公式；
(3)设Tn为数列{
}的前n项和，问是否存在正整数m，使得对任意的n∈N*，有Tn＜
成立？若存在，求出m的最小值；若不存在，则说明理由．
答案：
解析：
解析：
|
解：(1)令x＝y＝0，得f(0)＝0． 又当x＝0时，f(0)－f(y)＝f(－y)，即f(－y)＝－f(y)． ∴对任意x∈(－1，1)时，都有f(－x)＝－f(x)．∴f(x)为奇函数． (2)∵{xn}满足x1＝ ∴0＜xn＜1．∴f(xn+1)＝f ∵f(x)在(－1，1)上是奇函数，∴f(－xn)＝－f(xn)，∴f(xn+1)＝2f(xn)，即 ∴f(xn)＝2n－1． (3)Tn＝ 假设存在正整数m，使得对任意的n∈N*，有Tn＜ 只需 此时m的最小值为10． |
，xn+1＝
，
．
．∵{f(xn)}是以f(x1)＝f
＝1为首项，以2为公比的等比数列，
．
成立，即2－
对n∈N*恒成立．
≥2，即m≥10，故存在正整数m，使得对n∈N*，有Tn＜
成立．
练习册系列答案
相关题目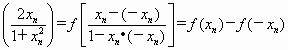