题目内容
设函数f(x)＝a－2－sin2x＋2(a－1)sinxcosx－5cos2x(a∈R，x∈R)．
(1)若a＝2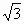
＋1，试说明y＝f(x)的图像可以由y＝sinx(x∈R)的图像经过怎样的平移和伸缩变换得到？
(2)是否存在常数a使得不等式|f(x)|≤6对任意的x∈R成立？若成立，求出a的取值范围；若不存在，请说明理由．
答案：
解析：
解析：
|
f(x)＝a－2－ (1)因为a＝2 f(x)＝2 所以由y＝sinx图像上的每一点的横坐标缩短为原来的 (2)f(x)＝ 所以 解得1≤a≤ |
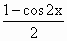＋(a－1)sin2x－
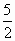(1＋cos2x)＝(a－1)sin2x－2cos2x＋a－5
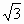＋1，所以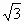
sin2x－2cos2x＋2
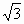－4＝4sin(2x－
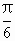)＋2
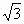－4＝4sin[2(x－
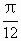)]＋2
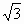－4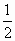
(纵坐标不变)得到y＝sin2x的图像，再将所得的图像上的每一点的纵坐标伸长到原来的4倍(横坐标不变)，得到y＝4sin2x的图像，又向右平移
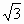个单位，即能得到f(x)的图像．
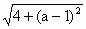sin(2x－
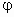)＋a－5，依题意，x∈R时，－6≤f(x)≤6，
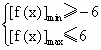即
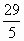，此即所求的a的取值范围．
练习册系列答案
相关题目
已知向量a＝(cos
x，sinx)，b＝(cos
，sin)，c＝(
，－1)，其中x∈R，
(1)当a·b＝
时，求x值的集合；
(2)设函数f(x)＝(a－c)2，求f(x)的最小正周期及其单调增区间.
已知向量a＝(cos
x，sin
，sin
，－1)，其中x∈R，
时，求x值的集合；
sin2x＋m)．
时，－4<f(x)<4恒成立，求实数m的取值范围．