Question

6．已知△ABC是边长为2的正三角形，点P是△ABC内一点，且$\overrightarrow{PA}$+2$\overrightarrow{PB}$+3$\overrightarrow{PC}$=$\overrightarrow{0}$．则$\overrightarrow{PA}$•$\overrightarrow{PB}$等于（　　）

• A． -$\frac{2}{9}$
• B． -$\frac{1}{9}$
• C． $\frac{2}{9}$
• D． $\frac{8}{9}$

Answer 1

分析 根据已知条件即可得到$\overrightarrow{PA}+\overrightarrow{PC}=-2（\overrightarrow{PB}+\overrightarrow{PC}）$，可画出图形，取AC边中点D，BC边中点E，所以可得到$\overrightarrow{PD}=-2\overrightarrow{PE}$，所以DE为△ABC的中位线，而$\overrightarrow{PA}=\overrightarrow{PD}+\overrightarrow{DA}$，$\overrightarrow{PB}=\overrightarrow{PE}+\overrightarrow{EB}$，所以$\overrightarrow{PA}•\overrightarrow{PB}=\overrightarrow{PD}•\overrightarrow{PE}+\overrightarrow{PD}•\overrightarrow{EB}$$+\overrightarrow{DA}•\overrightarrow{PE}+\overrightarrow{DA}•\overrightarrow{EB}$，进行数量积的运算即可．

解答 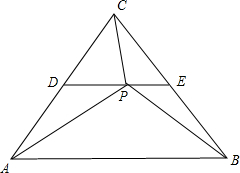解：如图，取AC中点D，BC中点E；
∵$\overrightarrow{PA}+2\overrightarrow{PB}+3\overrightarrow{PC}=\overrightarrow{0}$；
∴$\overrightarrow{PA}+\overrightarrow{PC}=-2（\overrightarrow{PB}+\overrightarrow{PC}）$；
∴$2\overrightarrow{PD}=-4\overrightarrow{PE}$；
∴$\overrightarrow{PD}=-2\overrightarrow{PE}$；
∴P，D，E三点共线，DE为△ABC的中位线；
∴$|\overrightarrow{PD}|=\frac{2}{3}，|\overrightarrow{PE}|=\frac{1}{3}$；
∴$\overrightarrow{PA}•\overrightarrow{PB}$=$（\overrightarrow{PD}+\overrightarrow{DA}）•（\overrightarrow{PE}+\overrightarrow{EB}）$=$\overrightarrow{PD}•\overrightarrow{PE}+\overrightarrow{PD}•\overrightarrow{EB}$$+\overrightarrow{DA}•\overrightarrow{PE}+\overrightarrow{DA}•\overrightarrow{EB}$=$-\frac{2}{9}+\frac{2}{3}•1•（-\frac{1}{2}）+1•\frac{1}{3}•（-\frac{1}{2}）+1•1•\frac{1}{2}=-\frac{2}{9}$．
故选：A．

点评 考查向量加法的平行四边形法则，共线向量基本定理，向量加法的几何意义，以及数量积的计算公式．