题目内容
(本题满分12分)已知函数y=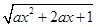 的定义域为R,解关于x的不等式
的定义域为R,解关于x的不等式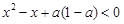
【答案】
当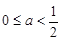 时,
时,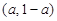 ;当
;当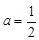 时,Ф;当
时,Ф;当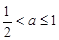 时,
时,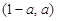 .
.
【解析】
试题分析:由条件可得0≤a≤1,原不等式可化为(x-a)[x-(1-a)]>0,分0≤a<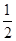 、a=
、a=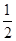 、
、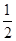 <a≤1三种情况,分别求出不等式的解集.
<a≤1三种情况,分别求出不等式的解集.
解:∵函数y=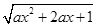 的定义域为R,∴
的定义域为R,∴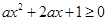 恒成立. …1分
恒成立. …1分
当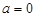 时,
时,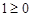 ,不等式恒成立;当
,不等式恒成立;当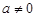 时,则
时,则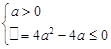
解得 .综上,
.综上,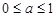 ………………………4分
………………………4分
由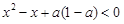 得
得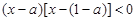 .……6分
.……6分
∵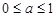 ,
,
∴(1)当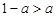 ,即
,即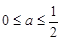 时,
时,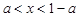 ;
;
(2)当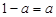 ,即
,即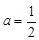 时,
时,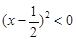 ,不等式无解;
,不等式无解;
(3)当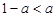 ,即
,即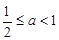 时,
时,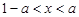 .………………………………10分
.………………………………10分
∴原不等式的解集为:当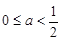 时,
时,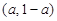 ;当
;当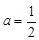 时,Ф;当
时,Ф;当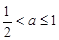 时,
时,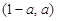 .
……………………12分
.
……………………12分
考点:本试题主要考查了二元一次不等式的解法,函数的恒成立问题,体现了分类讨论的数学思想,属于中档题.
点评:解决该试题的关键是由条件可得0≤a≤1,对于参数a,分0≤a<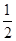 、a=
、a=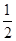 、
、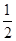 <a≤1三种情况,分别求出不等式的解集.
<a≤1三种情况,分别求出不等式的解集.

练习册系列答案
相关题目
 的三个内角
的三个内角 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、 .
. ,且
,且 .(1)求
.(1)求 .求
.求 .
. ,
, 的等比中项。
的等比中项。 是等差数列;(2)若
是等差数列;(2)若 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。 :
: 的长轴长是短轴长的
的长轴长是短轴长的 倍,
倍, ,
, 是它的左,右焦点.
是它的左,右焦点. ,且
,且 ,
, ,求
,求 作以
作以 (
( 是切点),且使
是切点),且使 ,求动点
,求动点 的长轴,短轴端点分别是A,B,从椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点,向量
的长轴,短轴端点分别是A,B,从椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点,向量 与
与 是共线向量
是共线向量 分别是左右焦点,求
分别是左右焦点,求 的取值范围
的取值范围