题目内容
 (2012•浦东新区二模)如图,在直三棱柱ABC-A1B1C1中,BA⊥BC.
(2012•浦东新区二模)如图,在直三棱柱ABC-A1B1C1中,BA⊥BC.(1)若BA=BB1,求证:AB1⊥平面A1BC;
(2)若BA=BC=BB1=2,M是棱BC上的一动点.试确定点M的位置,使点M到平面A1B1C的距离等于
| ||
| 2 |
分析:(1)当BA=BB1时,AB1⊥A1B.由BC⊥BA,BC⊥BB1,且BA∩BB1=B,知BC⊥平面ABB1.由此能证明AB1⊥平面A1BC.
(2)建立空间直角坐标系,得C(0,0,2)、B1(0,2,0)、A1(2,2,0)、设M(0,0,h).设平面A1B1C的法向量为
=(u , v , w),则
⊥
,
⊥
.得平面A1B1C的一个法向量为
=(0 , 1 , 1),由此能求出点M到平面A1B1C的距离.
(2)建立空间直角坐标系,得C(0,0,2)、B1(0,2,0)、A1(2,2,0)、设M(0,0,h).设平面A1B1C的法向量为
| n |
| n |
| CB1 |
| n |
| A1B1 |
| n |
解答:(1)证明:当BA=BB1时,AB1⊥A1B.
又∵BC⊥BA,BC⊥BB1,且BA∩BB1=B,
∴BC⊥平面ABB1.
而AB1?平面ABB1,∴AB1⊥BC.
∴由
,
得到AB1⊥平面A1BC.
(2)解:如图所示,建立空间直角坐标系,
可得有关点的坐标为C(0,0,2)、B1(0,2,0)、A1(2,2,0),
设M(0,0,h).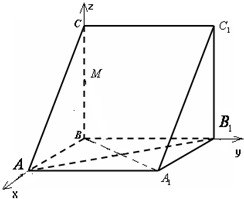 设平面A1B1C的法向量为
设平面A1B1C的法向量为
=(u , v , w),
则
⊥
,
⊥
.
∵
=(0,2,-2),
=(-2 , 0 , 0),
且
•
=0 ,
•
=0,
∴
,∴
,取ω=v=1,
得平面A1B1C的一个法向量为
=(0 , 1 , 1),
且|
|=
,又∵
=(0,2,-h),
于是点M到平面A1B1C的距离d=
=
=
=
⇒h=1,或h=3(舍)
所以,当点M为棱BC的中点时,点M到平面A1B1C的距离等于
.
又∵BC⊥BA,BC⊥BB1,且BA∩BB1=B,
∴BC⊥平面ABB1.
而AB1?平面ABB1,∴AB1⊥BC.
∴由
|
得到AB1⊥平面A1BC.
(2)解:如图所示,建立空间直角坐标系,
可得有关点的坐标为C(0,0,2)、B1(0,2,0)、A1(2,2,0),
设M(0,0,h).
 设平面A1B1C的法向量为
设平面A1B1C的法向量为| n |
则
| n |
| CB1 |
| n |
| A1B1 |
∵
| CB1 |
| A1B1 |
且
| n |
| CB1 |
| n |
| A1B1 |
∴
|
|
得平面A1B1C的一个法向量为
| n |
且|
| n |
| 2 |
| MB1 |
于是点M到平面A1B1C的距离d=
|
| ||||
|
|
| |0×0+1×2-h| | ||
|
| |2-h| | ||
|
| ||
| 2 |
所以,当点M为棱BC的中点时,点M到平面A1B1C的距离等于
| ||
| 2 |
点评:本题考查点、线、面间的距离的计算,解题时要认真审题,注意合理地化空间问题为平面问题,注意向量法的合理运用.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
 (2012•浦东新区二模)手机产业的发展催生了网络新字“孖”.某学生准备在计算机上作出其对应的图象,其中A(2,2),如图所示.在作曲线段AB时,该学生想把函数
(2012•浦东新区二模)手机产业的发展催生了网络新字“孖”.某学生准备在计算机上作出其对应的图象,其中A(2,2),如图所示.在作曲线段AB时,该学生想把函数