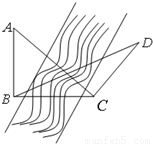
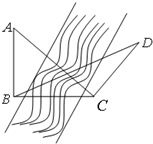
题目内容
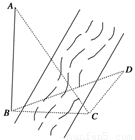
 如图,为测得河对岸塔AB的高,先在河岸上选一点C,使C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10米到位置D,测得∠BDC=45°,则塔AB的高是
如图,为测得河对岸塔AB的高,先在河岸上选一点C,使C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10米到位置D,测得∠BDC=45°,则塔AB的高是分析:设塔高为x米,根据题意可知在△ABC中,∠ABC=90°,∠ACB=60°,AB=x,从而有BC=
x,在△BCD中,CD=10,
∠BCD=105°,∠BDC=45°,∠CBD=30°,由正弦定理
=
可求 BC,从而可求x即塔高
| ||
| 3 |
∠BCD=105°,∠BDC=45°,∠CBD=30°,由正弦定理
| BC |
| sin∠BDC |
| CD |
| sin∠CBD |
解答:解:设塔高为x米,根据题意可知在△ABC中,∠ABC=90°,∠ACB=60°,AB=x,
从而有BC=
x,AC=
x
在△BCD中,CD=10,∠BCD=60°+30°+15°=105°,∠BDC=45°,∠CBD=30°
由正弦定理可得,
=
可得,BC=
=10
=
x
则x=10
故答案为:10
从而有BC=
| ||
| 3 |
2
| ||
| 3 |
在△BCD中,CD=10,∠BCD=60°+30°+15°=105°,∠BDC=45°,∠CBD=30°
由正弦定理可得,
| BC |
| sin∠BDC |
| CD |
| sin∠CBD |
可得,BC=
| 10sin45° |
| sin30° |
| 2 |
| ||
| 3 |
则x=10
| 6 |
故答案为:10
| 6 |
点评:本题主要考查了正弦定理在实际问题中的应用,解决本题的关键是要把实际问题转化为数学问题,结合已知把题目中的数据转化为三角形中的数据,进而选择合适的公式进行求解.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
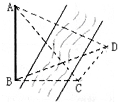 如图,为测得河对岸塔AB的高,先在河岸上选一点C,使在C塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10米到位置D,测得∠BDC=45°,则塔高AB的高度为( )
如图,为测得河对岸塔AB的高,先在河岸上选一点C,使在C塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10米到位置D,测得∠BDC=45°,则塔高AB的高度为( )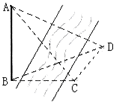 如图,为测得河对岸塔AB的高,先在河岸上选一点C,使C在塔底B的正东方向上,测得点A的仰角为60°,再由点C东偏北60°方向走10米到位置D,测得∠ADB=45°,则塔AB的高度为( )
如图,为测得河对岸塔AB的高,先在河岸上选一点C,使C在塔底B的正东方向上,测得点A的仰角为60°,再由点C东偏北60°方向走10米到位置D,测得∠ADB=45°,则塔AB的高度为( )