题目内容
如图，设抛物线C：y=x2的焦点为F，动点P在直线l：x-y-2=0上运动，过P作抛物线C的两条切线PA、PB，且与抛物线C分别相切于A、B两点．则△APB的重心G的轨迹方程为 ．
【答案】分析：欲求轨迹方程，可寻找被动点M的坐标（x，y）与主动点N的坐标（x，y）之间的关系，并用x，y表示x，y，再代入曲线C的方程即可；此法为“参数法”的一种，借助M、N两点坐标之间的关系及曲线C的方程消去两个参数x，y．
解答：解：设切点A、B坐标分别为（x，x2）和（x1，x12）（x1≠x），
∵y/=2x，∴两切线斜率分别为：2x和2x1，
于是：切线AP的方程为：2xx-y-x2=0
切线BP的方程为：2x1x-y-x12=0
解得P点的坐标为：xP=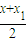
，yP=xx1
所以△APB的重心G的坐标为xG=
=xP，
yG=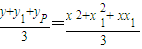
=
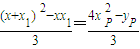
∴yP=-3yG+4xG2，结合xP=xG代入点P所在在直线方程，得到重心G的轨迹方程为：x-（-3y+4x2）-2=0，即y=
（4x2-x+2）．
点评：本题求轨迹的方法称为“代入法”，问题的基本结构是：动点N在已知曲线C上移动，动点M随之移动（伴随点），求动点M的轨迹方程．其求解可多参考本题分析中的一般解法．
解答：解：设切点A、B坐标分别为（x，x2）和（x1，x12）（x1≠x），
∵y/=2x，∴两切线斜率分别为：2x和2x1，
于是：切线AP的方程为：2xx-y-x2=0
切线BP的方程为：2x1x-y-x12=0
解得P点的坐标为：xP=
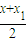，yP=xx1所以△APB的重心G的坐标为xG=
=xP，yG=
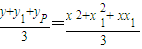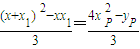
=∴yP=-3yG+4xG2，结合xP=xG代入点P所在在直线方程，得到重心G的轨迹方程为：x-（-3y+4x2）-2=0，即y=
（4x2-x+2）．点评：本题求轨迹的方法称为“代入法”，问题的基本结构是：动点N在已知曲线C上移动，动点M随之移动（伴随点），求动点M的轨迹方程．其求解可多参考本题分析中的一般解法．
练习册系列答案
相关题目
如图，设抛物线C：y=x2的焦点为F，动点P在直线l：x-y-2=0上运动，过P作抛物线C的两条切线PA、PB，且与抛物线C分别相切于A、B两点．则△APB的重心G的轨迹方程为