题目内容
求证:对任意x、y∈R,都有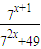 ≤5-3y+
≤5-3y+ y2,并说明等号何时成立.
y2,并说明等号何时成立.
【答案】分析:首先分析题目要求证明不等式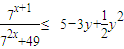 ,可对不等式两边分别做讨论,左边利用基本不等式可得
,可对不等式两边分别做讨论,左边利用基本不等式可得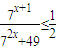 ,右边根据配方法得出
,右边根据配方法得出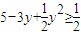 ,综合起来即得结果,当不等式两边都等于
,综合起来即得结果,当不等式两边都等于 的时候等号成立,解得x y的值即可.
的时候等号成立,解得x y的值即可.
解答:证明:首先利用基本不等式可得;72x+49≥2•7x•7=2•7x+1,
所以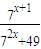 ≤
≤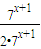 =
= .
.
又因为5-3y+ y2=
y2= (y-3)2+
(y-3)2+ ≥
≥ ,
,
所以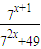 ≤5-3y+
≤5-3y+ y2.即得证.
y2.即得证.
当且仅当x=1,y=3时取等号.
点评:此题主要考查基本不等式的应用和由配方法求最值的问题,这2个知识点都属于重点考点且应用广泛,同学们需要多加注意.
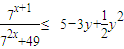 ,可对不等式两边分别做讨论,左边利用基本不等式可得
,可对不等式两边分别做讨论,左边利用基本不等式可得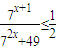 ,右边根据配方法得出
,右边根据配方法得出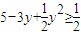 ,综合起来即得结果,当不等式两边都等于
,综合起来即得结果,当不等式两边都等于 的时候等号成立,解得x y的值即可.
的时候等号成立,解得x y的值即可.解答:证明:首先利用基本不等式可得;72x+49≥2•7x•7=2•7x+1,
所以
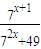 ≤
≤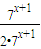 =
= .
.又因为5-3y+
 y2=
y2= (y-3)2+
(y-3)2+ ≥
≥ ,
,所以
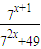 ≤5-3y+
≤5-3y+ y2.即得证.
y2.即得证.当且仅当x=1,y=3时取等号.
点评:此题主要考查基本不等式的应用和由配方法求最值的问题,这2个知识点都属于重点考点且应用广泛,同学们需要多加注意.

练习册系列答案
相关题目