题目内容
已知双曲线C的两条渐近线都过原点,且都以点A(![]() ,0)为圆心,1为半径的圆相切,双曲线的一个顶点A1与A点关于直线y=x对称.
,0)为圆心,1为半径的圆相切,双曲线的一个顶点A1与A点关于直线y=x对称.
(1)求双曲线C的方程.
(2)设直线l过点A,斜率为k,当0<k<1时,双曲线C的上支上有且仅有一点B到直线l的距离为![]() ,试求k的值及此时B点的坐标.
,试求k的值及此时B点的坐标.
(1) x2-y2=2, (2) B(2![]() ,
,![]() )
)
解析:
(1)设双曲线的渐近线为y=kx,由d=![]() =1,解得k=±1.
=1,解得k=±1.
即渐近线为y=±x,又点A关于y=x对称点的坐标为(0,![]() ).
).
∴a=![]() =b,所求双曲线C的方程为x2-y2=2.
=b,所求双曲线C的方程为x2-y2=2.
(2)设直线l: y=k(x-![]() )(0<k<1
)(0<k<1![]() ,
,
依题意B点在平行的直线l′上,且l与l′间的距离为![]() .
.
设直线l′:y=kx+m,应有![]() ,
,
化简得m2+2![]() km=2
km=2![]() ②
②
把l′代入双曲线方程得(k2-1)x2+2mkx+m2-2=0,
由Δ=4m2k2-4(k2-1)(m2-2)=0![]()
可得m2+2k2=2 ③
②、③两式相减得k=![]() m,代入③得m2=
m,代入③得m2=![]() ,解得m=
,解得m=![]() ,k=
,k=![]() ,
,
此时x=![]() ,y=
,y=![]()
![]() 故B(2
故B(2![]() ,
,![]() ).
).

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
 ,0)为右焦点的双曲线C的离心率,
,0)为右焦点的双曲线C的离心率,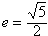 。
。