题目内容
(本小题共14分)
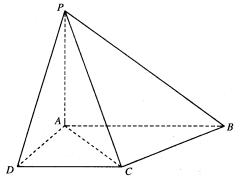
四棱锥P—ABCD中,PA⊥底面ABCD,AB//CD,AD=CD=1,∠BAD=120°,PA=![]() ,∠ACB=90°。
,∠ACB=90°。
(I)求证:BC⊥平面PAC;
(II)求二面角D—PC—A的大小;
(III)求点B到平面PCD的距离。
![]() ,
,![]()
解析:
解法一:
证明:(I)∵PA⊥底面ABCD,![]() 平面ABCD,
平面ABCD,
∴PA⊥BC
∵∠ACB=90°
∴BC⊥AC
又![]()
∴BC⊥平面PAC 4分
解:(II)∵AB//CD,∠DAB=120°
∴∠ADC=60°,又AD=CD=1
∴△ADC为等边三角形,且AC=1 5分
取AC的中点O,则DO⊥AC
∵PA⊥底面ABCD
∴PA⊥DO
∴DO⊥平面PAC
过O作OH⊥PC,垂足为H,连DH,由三垂线定理知DH⊥PC
∴∠DHO为二面角D—PC—A的平面角 7分
由![]() 8分
8分
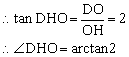
∴二面角D—PC—A的大小为arctan2 9分
(III)设点B到平面PCD的距离为d
∵AB//CD,![]() 平面PCD
平面PCD
∴AB//平面PCD
∴点B到平面PCD的距离等于点A到平面PCD的距离 11分
 13分
13分
![]() 14分
14分
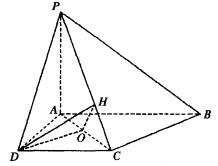
解法二:
证明:(I)同解法一 4分
解:(II)取CD的中点E,则AE⊥CD
∴AE⊥AB
又PA⊥底面ABCD,![]() 底面ABCD
底面ABCD
∴PA⊥AE 5分
建立空间直角坐标系,如图。则

A(0,0,0),![]()
![]()
![]() 7分
7分
设![]() 为平面PAC的一个法向量
为平面PAC的一个法向量
![]() 为平面PDC的一个法向量,则
为平面PDC的一个法向量,则
 ,
,
可取![]() ;
;
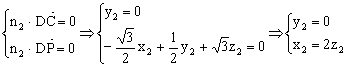 ,可取
,可取![]() 9分
9分
![]() 10分
10分

故所求二面角的大小为![]() 11分
11分
(III)又B(0,2,0),![]() 12分
12分
由(II)取平面PCD的一个法向量![]()
∴点B到平面PCD的距离为
![]() 13分
13分
 14分
14分
