题目内容
《莱因德纸草书》(Rhind Papyrus)是世界上最古老的数学著作之一。书中有一道这样的题目:把100个面包分给五人,使每人成等差数列,且使最大的三份之和的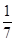 是较小的两份之和,则最小1份的大小是
是较小的两份之和,则最小1份的大小是

解析试题分析:设五个人所分得的面包为a-2d,a-d,a,a+d,a+2d,(其中d>0);
则,(a-2d)+(a-d)+a+(a+d)+(a+2d)=5a=100,∴a=20;
由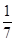 (a+a+d+a+2d)=a-2d+a-d,得3a+3d=7(2a-3d);∴24d=11a,∴d=
(a+a+d+a+2d)=a-2d+a-d,得3a+3d=7(2a-3d);∴24d=11a,∴d=
所以,最小的1分为a-2d=20-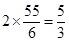 ,故答案为
,故答案为 。
。
考点:本题主要考查了等差数列模型的实际应用,解题时应巧设数列的中间项,从而容易得出结果
点评:解决该试题的关键是设五个人所分得的面包为a-2d,a-d,a,a+d,a+2d,(d>0);则由五个人的面包和为100,得a的值;由较大的三份之和的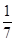 是较小的两份之和,得d的值;从而得最小的1分a-2d的值.
是较小的两份之和,得d的值;从而得最小的1分a-2d的值.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
传说古希腊毕达哥拉斯学派的数学家经常在沙滩上画点或用小石子表示数. 他们研究过如图所示的三角形数: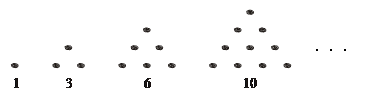
|
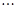 记为数列
记为数列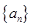 ,将可被5整除的三角形数按从小到大的顺序组成一个新数列
,将可被5整除的三角形数按从小到大的顺序组成一个新数列 . 可以推测:(Ⅰ)
. 可以推测:(Ⅰ)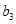 是数列
是数列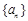 中的第 项;
中的第 项;(Ⅱ)
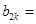 ________(用k表示)
________(用k表示) 设数列 的前n项和为
的前n项和为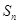 ,令
,令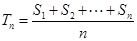 ,称
,称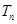 为数列
为数列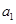 ,
,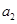 ,…,
,…, 的“理想数”,已知数列
的“理想数”,已知数列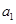 ,
,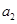 ,……,
,……,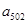 的“理想数”为2012,那么数列2,
的“理想数”为2012,那么数列2,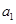 ,
,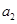 ,…,
,…,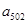 的“理想数”为( )
的“理想数”为( )
| A.2010 | B.2011 | C.2012 | D.2013 |
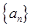 满足
满足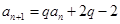 (
(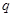 为常数,
为常数,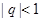 ),若
),若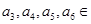
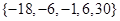 ,则
,则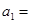 .
.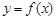 满足
满足 ,
,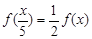 ,且当
,且当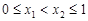 时,
时, ,则
,则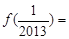 .
.
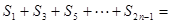 _______________。
_______________。 的各项都是正数,且对任意
的各项都是正数,且对任意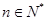 都有
都有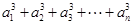
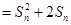 ,其中
,其中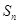 为数列
为数列 项和.
项和. 、
、 ;
;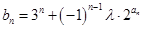 ,对任意的
,对任意的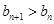 恒成立,求实数
恒成立,求实数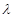 的取值范围.
的取值范围.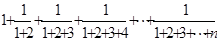 的前n项和
的前n项和 =
= 
 与所搭三角形的个数
与所搭三角形的个数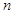 之间的关系式可以是
之间的关系式可以是