题目内容
已知函数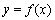 是R上的可导函数,当
是R上的可导函数,当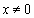 时,有
时,有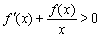 ,则函数
,则函数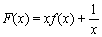 的零点个数是( )
的零点个数是( )
A.0 B.1 C. 2 D.3
【答案】
B
【解析】
试题分析: 当
当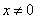 时,
时, 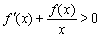 ,
,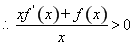 即
即
当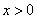 时,由
时,由 式知
式知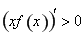 ,
,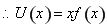 在
在 上为增函数,且
上为增函数,且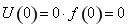 ,
,
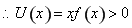 在
在 上恒成立.又
上恒成立.又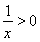 ,所以
,所以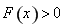 在
在 上恒成立.
上恒成立. 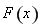 在
在 上无零点.当
上无零点.当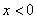 时,
时, 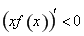 ,
,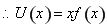 在
在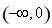 上为减函数,且
上为减函数,且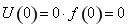 ,
,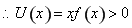 在
在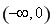 上恒成立.所以
上恒成立.所以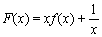 在在
在在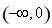 上为减函数,且当
上为减函数,且当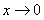 时,
时,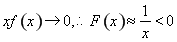 , 当
, 当 时,
时,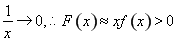 ,所以
,所以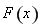 在
在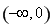 上有唯一零点.综上所述, 所以
上有唯一零点.综上所述, 所以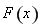 在
在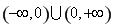 上有唯一零点.故选B.
上有唯一零点.故选B.
考点:1、导数与函数单调性的关系;2、函数的零点存在性;2、分类讨论的思想方法.

练习册系列答案
相关题目
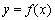
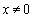


 满足:当
满足:当 时,
时,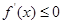 ;当
;当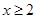 时,
时,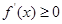 .则下列结论:①
.则下列结论:①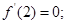 ②
②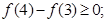 ③
③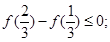 ④
④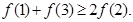 其中成立的个数是( )
其中成立的个数是( )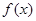 是R上的可导函数,且
是R上的可导函数,且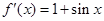 ,则函数
,则函数