题目内容
在极坐标系下,已知点A(-2,-
),B(
,
),O(0,0),则△ABO为( )
| π |
| 2 |
| 2 |
| 3π |
| 4 |
| A、正三角形 |
| B、直角三角形 |
| C、锐角等腰三角形 |
| D、直角等腰三角形 |
分析:先把极坐标系下的点A,B,C的坐标转化为直角坐标系下的点,然后根据两点就的距离公式可求,AC,AB,BC,从而可进行判断
解答:解:极坐标系下,点A(-2,-
),B(
,
),O(0,0),
则在直角坐标系下A(0,2),B(-1,1),C(0,0)
∴AC=2,AB=BC=
AC2=AB2+BC2
三角形ABO为等腰直角三角形
故选D.
| π |
| 2 |
| 2 |
| 3π |
| 4 |
则在直角坐标系下A(0,2),B(-1,1),C(0,0)
∴AC=2,AB=BC=
| 2 |
三角形ABO为等腰直角三角形
故选D.
点评:本题主要考查了三角形的形状的判断,解题的关键是要把极坐标系转化为直角坐标系,还要注意两点间的距离公式的应用.

练习册系列答案
相关题目
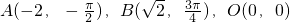 ,则△ABO为
,则△ABO为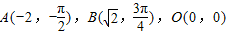 ,则△ABO为( )
,则△ABO为( )