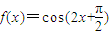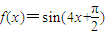题目内容
若函数f（x）同时具有以下两个性质：①f（x）是偶函数；②对任意实数x，都有f(
+x)=f(
-x)，则f（x）的解析式可以是（ ）
| π |
| 4 |
| π |
| 4 |
分析：考查各个选项中的函数是否是偶函数，且图象关于x=
对称，同时满足这两个条件的函数即为所求．
| π |
| 4 |
解答：解：由题意可得函数f（x）是偶函数且图象关于x=
对称．
由于f（x）=cos2x的图象的对称轴为2x=kπ，k∈z，即 x=
，k∈z，故不满足条件．
由于f（x）=cos(2x+
)=-sin2x，不是偶函数，故不满足条件．
由于f（x）=xos6x的对称轴为 6x=kπ，k∈z，即 x=
，k∈z，故不满足条件．
由于f（x）=sin（4x+
）=-cos4x，是偶函数，且对称轴为4x=kπ，k∈z，即 x=
，k∈z，故满足条件．
故选D．
| π |
| 4 |
由于f（x）=cos2x的图象的对称轴为2x=kπ，k∈z，即 x=
| kπ |
| 2 |
由于f（x）=cos(2x+
| π |
| 2 |
由于f（x）=xos6x的对称轴为 6x=kπ，k∈z，即 x=
| kπ |
| 6 |
由于f（x）=sin（4x+
| π |
| 2 |
| π |
| 4 |
故选D．
点评：本题考查三角函数的奇偶性和对称性，以及诱导公式的应用，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
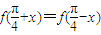，则f（x）的解析式可以是（ ）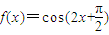
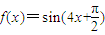
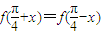，则f（x）的解析式可以是（ ）
