题目内容
已知 ,若存在
,若存在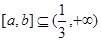 ,使得
,使得 ,则实数
,则实数 的取值范围是 .
的取值范围是 .
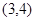
解析试题分析:因为存在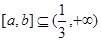 ,所以b>a>
,所以b>a>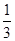 ,
,
而 是单调增函数,且
是单调增函数,且 时,其取值范围为(1,4)
时,其取值范围为(1,4)
所以,f(a)=ma,f(b)=mb
从而, =ma,
=ma,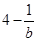 =mb,所以
=mb,所以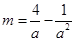 ,
,
设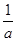 为t,则t属于(0,3),
为t,则t属于(0,3), 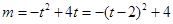 ,
,
又,m要使方程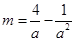 即
即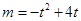 在(0,3)有两个根,所以结合函数图象得,
在(0,3)有两个根,所以结合函数图象得,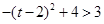 时,综上知,实数
时,综上知,实数 的取值范围是
的取值范围是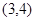 。
。
考点:本题主要考查二次函数的图象和性质。
点评:中档题,本题最终转化为二次函数的图象和性质,及一元二次方程根的分发布问题,易于忽视“在(0,3)有两个根”而出现错误。

练习册系列答案
相关题目
 的单调递减区间是 .
的单调递减区间是 .  米,
米, 米. 为了合理利用这块钢板,将在五边形
米. 为了合理利用这块钢板,将在五边形 内截取一个矩形块
内截取一个矩形块 ,使点
,使点 在边
在边 上. 则矩形
上. 则矩形 面积的最大值为____ 平方米 .
面积的最大值为____ 平方米 . 
 ,则
,则 的值等于
的值等于  对任意
对任意 都有
都有 ,且当
,且当 时,
时, ,则
,则 .
. 满足
满足 ,且
,且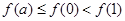 ,则实数
,则实数 的取值范围是_________.
的取值范围是_________. 在
在 为奇函数,
为奇函数, ,当
,当 时,
时, ,则
,则 。
。 ,
, ,则
,则 。
。 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时,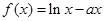 . 若函数
. 若函数 的取值范围是
的取值范围是