题目内容
已知动圆过定点(| p |
| 2 |
| p |
| 2 |
(Ⅰ)求动圆圆心C的轨迹的方程;
(Ⅱ)设A,B是轨迹C上异于原点O的两个不同点,直线OA和OB的倾斜角分别为α和β,当α,β变化且α+β为定值θ(0<θ<π且θ≠
| π |
| 2 |
分析:(I)设M为动圆圆心,(
,0)为记为F,过点M作直线x=-
的垂线,垂足为N,进而可知动点M到定点F与定直线x=-
的距离相等,进而推断点M的轨迹为抛物线,进而根据抛物线性质可得答案.
(II)设A(x1,y1),B(x2,y2),设其方程为y=kx+b,与抛物线方程联立,根据韦达定理表示出y1+y2,y1•y2,分θ=
和θ≠
时,求得直线方程,进而判断直线AB恒过是否定点.
| p |
| 2 |
| p |
| 2 |
| p |
| 2 |
(II)设A(x1,y1),B(x2,y2),设其方程为y=kx+b,与抛物线方程联立,根据韦达定理表示出y1+y2,y1•y2,分θ=
| π |
| 2 |
| π |
| 2 |
解答: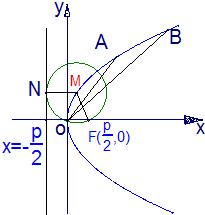 解:(I)如图,设M为动圆圆心,(
解:(I)如图,设M为动圆圆心,(
,0)为记为F,
过点M作直线x=-
的垂线,垂足为N,
由题意知:|MF|=|MN|,即动点M到定点F与定直线x=-
的距离相等,
由抛物线的定义知,点M的轨迹为抛物线,
其中F(
,0)为焦点,x=-
为准线,
所以轨迹方程为y2=2px(P>0);
(II)如图,设A(x1,y1),B(x2,y2),
由题意得x1≠x2(否则α+β=π)且x1,x2≠0.
所以直线AB的斜率存在,设其方程为y=kx+b,显然x1=
,x2=
.
将y=kx+b与y2=2px(p>0)联立消去x,得ky2-2py+2pb=0
由韦达定理知y1+y2=
,y1•y2=
①
(1)当θ=
时,即α+β=
时,tanα•tanβ=1.
所以
•
,x1x2-y1y2=0,
-y1y2=0.
所以y1y2=4p2
由①知:
=4p2,所以b=2pk.
因此直线AB的方程可表示为y=kx+2Pk.
即k(x+2P)-y=0所以直线AB恒过定点(-2p,0)
(2)当θ≠
时,由α+β=θ,得tanθ=tan(α+β)=
=
将①式代入上式整理化简可得:tanθ=
,所以b=
+2pk.
此时,直线AB的方程可表示为y=kx+
+2pk.即k(x+2p)-(y-
)=0.
所以直线AB恒过定点(-2p,
).
所以由(1)(2)知,当θ=
时,直线AB恒过定点(-2p,0),当θ≠
时直线AB恒过定点(-2p,
).
 解:(I)如图,设M为动圆圆心,(
解:(I)如图,设M为动圆圆心,(| p |
| 2 |
过点M作直线x=-
| p |
| 2 |
由题意知:|MF|=|MN|,即动点M到定点F与定直线x=-
| p |
| 2 |
由抛物线的定义知,点M的轨迹为抛物线,
其中F(
| p |
| 2 |
| p |
| 2 |
所以轨迹方程为y2=2px(P>0);
(II)如图,设A(x1,y1),B(x2,y2),
由题意得x1≠x2(否则α+β=π)且x1,x2≠0.
所以直线AB的斜率存在,设其方程为y=kx+b,显然x1=
| ||
| 2p |
| ||
| 2p |
将y=kx+b与y2=2px(p>0)联立消去x,得ky2-2py+2pb=0
由韦达定理知y1+y2=
| 2p |
| k |
| 2pb |
| k |
(1)当θ=
| π |
| 2 |
| π |
| 2 |
所以
| y1 |
| x1 |
| y2 |
| x2 |
| ||||
| 4p2 |
所以y1y2=4p2
由①知:
| 2pb |
| k |
因此直线AB的方程可表示为y=kx+2Pk.
即k(x+2P)-y=0所以直线AB恒过定点(-2p,0)
(2)当θ≠
| π |
| 2 |
| tanα+tanβ |
| 1-tanαtanβ |
| 2p(y1+y2) |
| y1y2-4p2 |
将①式代入上式整理化简可得:tanθ=
| 2p |
| b-2pk |
| 2p |
| tanθ |
此时,直线AB的方程可表示为y=kx+
| 2p |
| tanθ |
| 2p |
| tanθ |
所以直线AB恒过定点(-2p,
| 2p |
| tanθ |
所以由(1)(2)知,当θ=
| π |
| 2 |
| π |
| 2 |
| 2p |
| tanθ |
点评:本题主要考查了求轨迹方程的问题.涉及直线的抛物线的关系,常需要联立方程根据韦达定理找到解决问题的突破口.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目