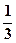题目内容
设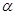 是直线
是直线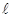 的倾斜角,向量
的倾斜角,向量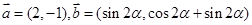 ,
,
若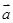 ⊥
⊥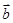 ,则直线
,则直线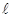 的斜率是( )
的斜率是( )
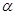 是直线
是直线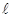 的倾斜角,向量
的倾斜角,向量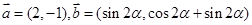 ,
,若
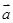 ⊥
⊥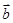 ,则直线
,则直线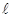 的斜率是( )
的斜率是( )| A.1 | B. | C. | D. |
B
先根据两个向量垂直得到sin(2α-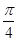 )=0;再结合α是直线l的倾斜角对应的范围即可求出α,进而求出直线的斜率.
)=0;再结合α是直线l的倾斜角对应的范围即可求出α,进而求出直线的斜率.
解:因为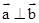 ,
,
∴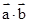 =0.
=0.
即 2sin2α+(-1)(cos2α+sin2α)=sin2α-cos2α=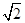 sin(2α-
sin(2α-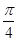 )=0.
)=0.
∵α是直线l的倾斜角
∴0≤α<π.
∴-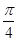 ≤2α-
≤2α-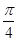 <
<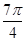 .
.
∴2α-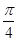 =0,π;
=0,π;
∴α=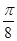 ,
,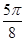 .
.
∴tanα有两个值.即直线的斜率有两种情况.
故选B.
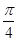 )=0;再结合α是直线l的倾斜角对应的范围即可求出α,进而求出直线的斜率.
)=0;再结合α是直线l的倾斜角对应的范围即可求出α,进而求出直线的斜率.解:因为
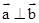 ,
,∴
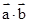 =0.
=0.即 2sin2α+(-1)(cos2α+sin2α)=sin2α-cos2α=
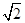 sin(2α-
sin(2α-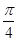 )=0.
)=0.∵α是直线l的倾斜角
∴0≤α<π.
∴-
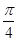 ≤2α-
≤2α-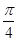 <
<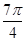 .
.∴2α-
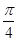 =0,π;
=0,π;∴α=
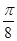 ,
,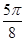 .
.∴tanα有两个值.即直线的斜率有两种情况.
故选B.

练习册系列答案
相关题目
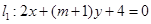 与直线
与直线 平行,则
平行,则 的值为( )
的值为( )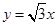 的距离与到
的距离与到 轴的距离相等的点的轨迹方程为 ( )
轴的距离相等的点的轨迹方程为 ( )

 或
或
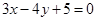 关于
关于 轴对称的直线方程为( )
轴对称的直线方程为( )


 的直线
的直线 平分了圆:
平分了圆: 的周长,则直线
的周长,则直线



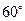 的直线被圆
的直线被圆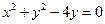 所截的弦长为_________
所截的弦长为_________ 与
与 轴、
轴、 轴分别交于
轴分别交于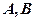 两点,若动点
两点,若动点 在线段
在线段 上,则
上,则 的最大值为
的最大值为  .
. 
 .
. 
 .
.
 .
.