题目内容
已知函数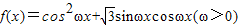 的最小正周期为π.
的最小正周期为π.(Ⅰ)求
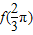 的值;
的值; (Ⅱ)求函数f(x)的单调递增区间及其图象的对称轴方程.
【答案】分析:(Ⅰ)利用两角差的正弦公式的应用,化简f(x)的解析式,和周期,即可求出ω,把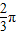 代入函数解析式即可求得结果;
代入函数解析式即可求得结果;
(II)根据正弦曲线的对称轴,写出函数的对称轴的形式,写出对称轴,根据正弦曲线的增区间,写出函数的增区间.
解答:解:(Ⅰ)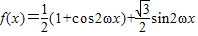
= ,
,
因为f(x)最小正周期为π,所以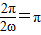 ,解得ω=1,
,解得ω=1,
所以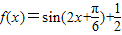 ,
,
所以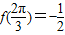 .
.
(Ⅱ)由 ,
,
得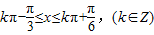 ,
,
所以,函数f(x)的单调增区间为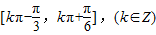 ;
;
由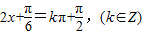 得
得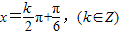 ,
,
所以,f(x)图象的对称轴方程为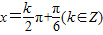 .
.
点评:本题考查三角函数的解析式和有关性质,是一个基础题,这种题目是高考卷中每一年都要出现的一种题目,注意题目的开始解析式不要出错.
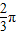 代入函数解析式即可求得结果;
代入函数解析式即可求得结果;(II)根据正弦曲线的对称轴,写出函数的对称轴的形式,写出对称轴,根据正弦曲线的增区间,写出函数的增区间.
解答:解:(Ⅰ)
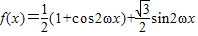
=
 ,
,因为f(x)最小正周期为π,所以
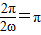 ,解得ω=1,
,解得ω=1,所以
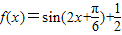 ,
,所以
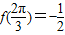 .
.(Ⅱ)由
 ,
,得
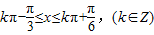 ,
,所以,函数f(x)的单调增区间为
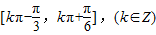 ;
;由
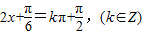 得
得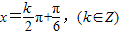 ,
,所以,f(x)图象的对称轴方程为
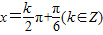 .
.点评:本题考查三角函数的解析式和有关性质,是一个基础题,这种题目是高考卷中每一年都要出现的一种题目,注意题目的开始解析式不要出错.

练习册系列答案
相关题目
 的最小正周期为
的最小正周期为 ,将其图象向左平移
,将其图象向左平移 个单位长度,所得图象关于
个单位长度,所得图象关于 轴对称,则
轴对称,则 的一个可能值是
( )
的一个可能值是
( ) B.
B. C.
C. D.
D.
 的最小正周期为2π.
的最小正周期为2π. ,求
,求 的值.
的值. 的最小正周期为π,其图象关于直线
的最小正周期为π,其图象关于直线 对称.
对称. 上的单调递增区间;
上的单调递增区间; 上只有一个实数解,求实数m的取值范围.
上只有一个实数解,求实数m的取值范围. 的最小正周期为
的最小正周期为 .
.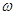 的值;
的值; 的最小正周期为
的最小正周期为
 的值;
的值;
 在
在
 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.