题目内容
一个棱长为8cm的密封正方体盒子中放一个半径为1cm的小球,无论怎样摇动盒子,则小球在盒子中不能到达的空间体积为 .

解析试题分析:小球在盒子不能到达的空间要分以下几种情况,在正方体顶点处的小正方体中,其体积等于小正方体体积减球的体积,在棱长处对应的正方体中,其体积等于这些小正方体体积的和减以球的直径为底面直径,以正方体和的高为高的圆柱,其他空间小球均能到达,综合后即可得到结果.解:在正方体的8个顶点处的单位立方体空间内,小球不能到达的空间为:8[13- (
( ×13)]=8-
×13)]=8- ,除此之外,在以正方体的棱为一条棱的12个1×1×6的正四棱柱空间内,小球不能到达的空间共为 [1×1×6-
,除此之外,在以正方体的棱为一条棱的12个1×1×6的正四棱柱空间内,小球不能到达的空间共为 [1×1×6- (π×12)×6]=72-18π.其他空间小球均能到达.故小球不能到达的空间体积为
(π×12)×6]=72-18π.其他空间小球均能到达.故小球不能到达的空间体积为 =
=
考点:球的体积
点评:本题考查的知识点是球的体积,棱柱的体积,其中熟练掌握棱柱和不堪的几何特征,建立良好的空间想象能力是解答本题的关键.

练习册系列答案
相关题目

 的边长为
的边长为 ,延长
,延长 至
至 ,使
,使 ,连接
,连接  、
、 , 则
, 则


 的棱长为6,则以正方体
的棱长为6,则以正方体 截正方体外接球所得的圆为底面的圆锥的表面积为__________
截正方体外接球所得的圆为底面的圆锥的表面积为__________ ,如果圆锥的体积恰好也与球的体积相等,那么这个圆锥的母线长为
,如果圆锥的体积恰好也与球的体积相等,那么这个圆锥的母线长为  .
. 
 中,
中, 分别为
分别为 的中点,则异面直线
的中点,则异面直线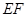 与
与 所成的角等于 .
所成的角等于 .