题目内容
函数f(x)=|sin2x|+|cos2x|(Ⅰ)求f(-
| 7π |
| 12 |
(Ⅱ)当x∈[0,
| π |
| 4 |
(Ⅲ)我们知道,函数的性质通常指函数的定义域、值域、周期性、奇偶性、单调性等,请你探究函数f(x)的性质(本小题只需直接写出结论)
分析:(I)把所给的自变量的值代入函数式,根据诱导公式化简整理出结果.
(II)对函数式进行整理,得到y=Asin(ωx+φ)的形式,根据所给的角的范围写出ωx+φ的范围,根据三角函数的图象得到函数的值域.
(III)根据上一问整理出的函数的解析式,得到函数的定义域、值域、周期性、奇偶性、单调性等.
(II)对函数式进行整理,得到y=Asin(ωx+φ)的形式,根据所给的角的范围写出ωx+φ的范围,根据三角函数的图象得到函数的值域.
(III)根据上一问整理出的函数的解析式,得到函数的定义域、值域、周期性、奇偶性、单调性等.
解答:解:(Ⅰ)f(-
)= |sin(-
)|+|cos(-
)| = |sin
|+|-cos
| =
2分
(Ⅱ)当x∈[0,
]时,2x∈[0,
],则sin2x≥0,cos2x≥0…3分
∴f(x)=sin2x+cos2x=
sin(2x+
)…5分
又∵x∈[0,
]
∴2x+
∈[
,
]∴sin(2x+
)∈[
,1]
∴当x∈[0,
]时,f(x)的取值范围为[1,
]. …7分
(Ⅲ)①f(x)的定义域为R; …8分
②∵f(-x)=|sin(-2x)|+|cos(-2x)|=|sin2x|+|cos2x|=f(x)∴f(x)为偶函数. …9分
③∵f(x+
)= |sin(2x+
)|+|cos(2x+
)| = |cos2x|+|sin2x| =f(x),
∴f(x)是周期为
的周期函数; …11分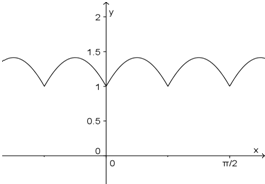
④由(Ⅱ)可知,当x∈[0,
]时,f(x)=
sin(2x+
),
∴值域为[1,
]. …12分
⑤可作出f(x)图象,如图所示:
由图象可知f(x)的增区间为[
,
+
](k∈Z),
减区间为[
+
,
+
](k∈Z) …14分
| 7π |
| 12 |
| 7π |
| 6 |
| 7π |
| 6 |
| π |
| 6 |
| π |
| 6 |
1+
| ||
| 2 |
(Ⅱ)当x∈[0,
| π |
| 4 |
| π |
| 2 |
∴f(x)=sin2x+cos2x=
| 2 |
| π |
| 4 |
又∵x∈[0,
| π |
| 4 |
∴2x+
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
| ||
| 2 |
∴当x∈[0,
| π |
| 4 |
| 2 |
(Ⅲ)①f(x)的定义域为R; …8分
②∵f(-x)=|sin(-2x)|+|cos(-2x)|=|sin2x|+|cos2x|=f(x)∴f(x)为偶函数. …9分
③∵f(x+
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
∴f(x)是周期为
| π |
| 4 |

④由(Ⅱ)可知,当x∈[0,
| π |
| 4 |
| 2 |
| π |
| 4 |
∴值域为[1,
| 2 |
⑤可作出f(x)图象,如图所示:
由图象可知f(x)的增区间为[
| kπ |
| 4 |
| π |
| 8 |
| kπ |
| 4 |
减区间为[
| π |
| 8 |
| kπ |
| 4 |
| π |
| 4 |
| kπ |
| 4 |
点评:本题考查三角函数的恒等变形及三角函数的性质,本题考查三角函数利用公式 asinx+bcosx=
sin(x+θ)化简,再进行三角函数的性质的运算.
| a2+b2 |

练习册系列答案
相关题目