题目内容
对于下列两个结论：
（1）把函数y=3sin(2x+
)的图象向右平移
得到y=3sin2x的图象；
（2）在△ABC中，若acosB=bcosA，则△ABC是等腰三角形．
则下面的判断正确的是（ ）
（1）把函数y=3sin(2x+
| π |
| 3 |
| π |
| 6 |
（2）在△ABC中，若acosB=bcosA，则△ABC是等腰三角形．
则下面的判断正确的是（ ）
| A．（1）（2）都正确 | B．（1）（2）都错误 | C．只有（1）正确 | D．只有（2）正确 |
先看（1），
∵设y=f（x）=3sin(2x+
)，则将函数y=3sin(2x+
)的图象向右平移
，
得到y=f（x-
）=3sin[2(x-
)+
]的图象，即y=3sin2x的图象．故（1）正确；
再看（2），
∵在△ABC中，acosB=bcosA，∴根据正弦定理得sinAcosB=sinBcosA，
两边都除以cosAcosB，得tanA=tanB
∵A、B都是三角形内角，∴A=B，得a=b，所以△ABC是等腰三角形．故（2）正确
故选：A
∵设y=f（x）=3sin(2x+
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
得到y=f（x-
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
再看（2），
∵在△ABC中，acosB=bcosA，∴根据正弦定理得sinAcosB=sinBcosA，
两边都除以cosAcosB，得tanA=tanB
∵A、B都是三角形内角，∴A=B，得a=b，所以△ABC是等腰三角形．故（2）正确
故选：A
练习册系列答案
小学数学口算题卡脱口而出系列答案
优秀生应用题卡口算天天练系列答案
浙江之星课时优化作业系列答案
相关题目
对于下列两个结论：
（1）把函数y=3sin(2x+
)的图象向右平移
得到y=3sin2x的图象；
（2）在△ABC中，cosB+cosC=
+
．，a，b，c分别为角A，B，C的对边），则△ABC的形状为直角三角形．
则下面的判断正确的是（ ）
（1）把函数y=3sin(2x+
| π |
| 3 |
| π |
| 6 |
（2）在△ABC中，cosB+cosC=
| b |
| a |
| c |
| a |
则下面的判断正确的是（ ）
| A、（1）（2）都正确 |
| B、（1）（2）都错误 |
| C、只有（1）正确 |
| D、只有（2）正确 |
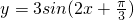的图象向右平移
得到y=3sin2x的图象；（2）在△ABC中，cosB+cosC=
+
．，a，b，c分别为角A，B，C的对边），则△ABC的形状为直角三角形．则下面的判断正确的是
的图象向右平移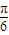
得到y=3sin2x的图象；