题目内容
对于下列两个结论:
(1)把函数y=3sin(2x+
)的图象向右平移
得到y=3sin2x的图象;
(2)在△ABC中,cosB+cosC=
+
.,a,b,c分别为角A,B,C的对边),则△ABC的形状为直角三角形.
则下面的判断正确的是( )
(1)把函数y=3sin(2x+
| π |
| 3 |
| π |
| 6 |
(2)在△ABC中,cosB+cosC=
| b |
| a |
| c |
| a |
则下面的判断正确的是( )
| A、(1)(2)都正确 |
| B、(1)(2)都错误 |
| C、只有(1)正确 |
| D、只有(2)正确 |
分析:根据函数图象平移左加又减的原则,可知(1)中的结论正确,利用余弦定理分别求得cosB,和cosC代入cosB+cosC=
+
,化简整理的a2=b2+c2,进而推断出三角形形状为直角三角形.
| b |
| a |
| c |
| a |
解答:解:根据函数图象平移左加又减的原则,
可知函数y=3sin(2x+
)的图象向右平移
得到y=3sin2x.故(1)结论正确.
由余弦定理:
cosB=
(a2+c2-b2)
cosC=
(a2+b2-c2)
∵cosB+cosC=
+
,
∴=
(a2+c2-b2)+
(a2+b2-c2)=
+
,
约去a
左边×2bc通分,那么右边也需×2bc
化简一步得
a2b-b3+a2c-c3=b2c+bc2
移项,
a2(b+c)=b2(b+c)+c2(b+c)
约分
a2=b2+c2,
∴△ABC的形状为直角三角形结论(2)正确.
故选A
可知函数y=3sin(2x+
| π |
| 3 |
| π |
| 6 |
由余弦定理:
cosB=
| 1 |
| 2ac |
cosC=
| 1 |
| 2ab |
∵cosB+cosC=
| b |
| a |
| c |
| a |
∴=
| 1 |
| 2ac |
| 1 |
| 2ab |
| b |
| a |
| c |
| a |
约去a
左边×2bc通分,那么右边也需×2bc
化简一步得
a2b-b3+a2c-c3=b2c+bc2
移项,
a2(b+c)=b2(b+c)+c2(b+c)
约分
a2=b2+c2,
∴△ABC的形状为直角三角形结论(2)正确.
故选A
点评:本题主要考查三角函数图象的平移,余弦定理的应用.考查了学生综合把握所学知识解决实际问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
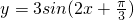 的图象向右平移
的图象向右平移 得到y=3sin2x的图象;(2)在△ABC中,cosB+cosC=
得到y=3sin2x的图象;(2)在△ABC中,cosB+cosC= +
+ .,a,b,c分别为角A,B,C的对边),则△ABC的形状为直角三角形.则下面的判断正确的是
.,a,b,c分别为角A,B,C的对边),则△ABC的形状为直角三角形.则下面的判断正确的是 的图象向右平移
的图象向右平移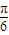 得到y=3sin2x的图象;
得到y=3sin2x的图象;