题目内容
【题目】在平面直角坐标系xOy中,已知抛物线C:![]() 的焦点为F,过F的直线
的焦点为F,过F的直线![]() 交抛物线C于A,B两点.
交抛物线C于A,B两点.
(1)求线段AF的中点M的轨迹方程;
(2)已知△AOB的面积是△BOF面积的3倍,求直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)设线段AF的中点的坐标为![]() ,
,![]() ,即可求得
,即可求得![]() ,将它们代入
,将它们代入![]() 即可得解。
即可得解。
(2)设![]() ,由△AOB的面积是△BOF面积的3倍可得:直线
,由△AOB的面积是△BOF面积的3倍可得:直线![]() 的斜率存在,且
的斜率存在,且![]() 的面积是
的面积是![]() 面积的2倍,即可整理得:
面积的2倍,即可整理得:![]() ,设直线
,设直线![]() 的方程为:
的方程为:![]() ,联立直线方程与抛物线方程可得:
,联立直线方程与抛物线方程可得:![]() ,
,![]() ,结合
,结合![]() 即可求得:
即可求得:![]() ,问题得解。
,问题得解。
(1)设线段AF的中点的坐标为![]() ,
,![]()
由抛物线![]() 的方程
的方程![]() 可得:焦点
可得:焦点![]()
由中点坐标公式可得:![]()
即:![]()
又![]() 在抛物线
在抛物线![]() 上,所以
上,所以![]() ,
,
将![]() 代入上式可得:
代入上式可得:![]()
整理得:![]()
所以线段AF的中点M的轨迹方程为:![]()
(2)依据题意作出图形,如下:
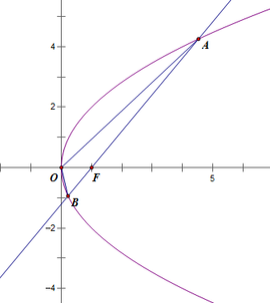
设![]() ,且
,且![]() 与
与![]() 的取值一正、一负
的取值一正、一负
因为△AOB的面积是△BOF面积的3倍,所以直线![]() 的斜率存在,
的斜率存在,
且![]() 的面积是
的面积是![]() 面积的2倍,
面积的2倍,
即:![]() ,整理得:
,整理得:![]()
设直线![]() 的方程为:
的方程为:![]()
联立直线与抛物线方程可得:![]() ,整理得:
,整理得:![]() .
.
所以![]() ,
,![]()
由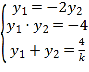 解得:
解得:![]() .
.
所以直线![]() 的方程为:
的方程为:![]()

 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案【题目】某市场研究人员为了了解产业园引进的甲公司前期的经营状况,采集相应数据,对该公司2017年连续六个月的利润进行了统计,并绘制了相应的折线图,如图所示:
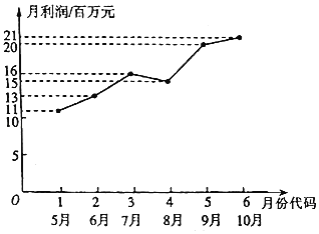
(1)折线图可以看出,可用线性回归模型拟合月利润![]() (单位:百万元)与月份代码
(单位:百万元)与月份代码![]() 之间的关系,求
之间的关系,求![]() 关于
关于![]() 的线性回归方程,并预测该公司2018年1月份的利润;
的线性回归方程,并预测该公司2018年1月份的利润;
(2)甲公司新研制了一款产品,需要采购一批新型材料,现有采购成本分别为10万元![]() 包和12万元
包和12万元![]() 包的
包的![]() 、
、![]() 两种型号的新型材料可供选择,按规定每种新型材料最多可使用4个月,不同类型的新型材料损坏的时间各不相同,已知生产新型材料的企业乙对
两种型号的新型材料可供选择,按规定每种新型材料最多可使用4个月,不同类型的新型材料损坏的时间各不相同,已知生产新型材料的企业乙对![]() 、
、![]() 两种型号各100件新型材料进行过科学模拟测试,得到两种新型材料使用寿命频数统计如表:
两种型号各100件新型材料进行过科学模拟测试,得到两种新型材料使用寿命频数统计如表:
使用寿命 材料类型 | 1个月 | 2个月 | 3个月 | 4个月 | 总计 |
| 20 | 35 | 35 | 10 | 100 |
| 10 | 30 | 40 | 20 | 100 |
经甲公司测算,平均每包新型材料每月可以带来5万元收入,不考虑除采购成本之外的其他成本,假设每包新型材料的使用寿命都是整数月,且以频率作为每包新型材料使用寿命的概率,如果你是甲公司的负责人,以每包新型材料产生利润的期望值为决策依据,你会选择采购哪款新型材料?
参考数据:![]() ,
,![]() .
.
参考公式:回归直线方程为![]() ,其中
,其中 .
.
【题目】京剧是我国的国粹,是“国家级非物质文化遗产”,为纪念著名京剧表演艺术家,京剧艺术大师梅兰芳先生,某电视台《我爱京剧》的一期比赛中,2位“梅派”传人和4位京剧票友(资深业余爱好者)在幕后登台演唱同一曲目《贵妃醉酒》选段,假设6位演员的演唱水平相当,由现场40位大众评委和“梅派”传人的朋友猜测哪两位是真正的“梅派”传人.
(1)此栏目编导对本期的40位大众评委的年龄和对京剧知识的了解进行调查,根据调查得到的数据如下:
京剧票友 | 一般爱好者 | 合计 | |
50岁以上 | 15 | 10 | 25 |
50岁以下 | 3 | 12 | 15 |
合计 | 18 | 22 | 40 |
试问:在犯错误的概率不超过多少的前提下,可以认为年龄的大小与对京剧知识的了解有关系?
(2)若在一轮中演唱中,每猜出一位亮相一位,且规定猜出2位“梅派”传人”或猜出5人后就终止,记本轮竞猜一共竞猜![]() 次,求随机变量
次,求随机变量![]() 的分布列与期望.
的分布列与期望.
参考数据:
0.50 | 0.40 | 0.25 | 0.15 | 0.10 |
0.455 | 0.708 | 1.323 | 2.072 | 2.706 |
0.05 | 0.025 | 0.005 | 0.001 | |
3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]()