Question

16.已知F₁、F₂为双曲线=1(a＞0，b＞0且a≠b)的两个焦点，P为双曲线右支上异于顶点的任意一点，O为坐标原点.下面四个命题

(A)△PF₁F₂的内切圆的圆心必在直线x=a上；

(B)△PF₁F₂的内切圆的圆心必在直线x=b上；

(C)△PF₁F₂的内切圆的圆心必在直线OP上；

(D)△PF₁F₂的内切圆必通过点(a，0).

    其中真命题的代号是__________(写出所有真命题的代号).

Answer 1

（A）（D）

解析：内切圆圆心为△PF₁F₂各角平分线交点，而OP为中点，二者不重合，从而C错.

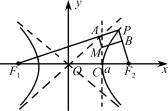
如图M为内心，ABC为内切圆与各边切点，则

F₁C+CF₂=2C

F₁C-CF₂=F₁A-BF₂=F₁P-PF₂=2a

从而F₁C=a+C

C点横坐标为a.从而A、D对B错.