题目内容
(本题满分12分)
双曲线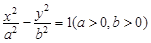 的左、右焦点分别为
的左、右焦点分别为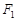 、
、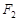 ,
,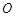 为坐标原点,点
为坐标原点,点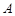 在双曲线的右支上,点
在双曲线的右支上,点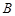 在双曲线左准线上,
在双曲线左准线上,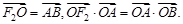
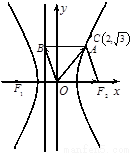
(Ⅰ)求双曲线的离心率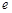 ;
;
(Ⅱ)若此双曲线过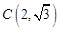 ,求双曲线的方程;
,求双曲线的方程;
(Ⅲ)在(Ⅱ)的条件下,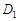 、
、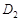 分别是双曲线的虚轴端点(
分别是双曲线的虚轴端点(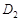 在
在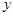 轴正半轴上),过
轴正半轴上),过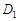 的直线
的直线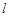 交双曲线
交双曲线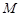 、
、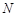 ,
,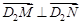 ,求直线
,求直线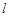 的方程
的方程
【答案】
(Ⅰ)2
(Ⅱ)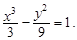
(Ⅲ)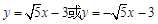
【解析】解:(Ⅰ)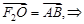 四边形
四边形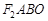 是平行四边形,
是平行四边形,
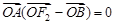 即
即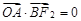 ,
,
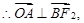 ∴平行四边形
∴平行四边形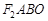 是菱形.
是菱形.
如图,则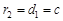 ,
, ,
,
由双曲线定义得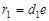

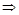
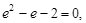
 (
(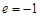 舍去) …………3分
舍去) …………3分
(Ⅱ)由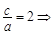
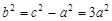 ,
,
双曲线方程为
把点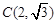 代入有得
代入有得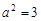 ,
,
∴双曲线方程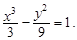 ………6分
………6分
(Ⅲ)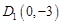 ,
,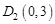 ,设
,设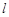 的方程为
的方程为
则由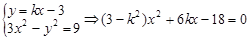 ,
,
因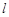 与与双曲线有两个交点,
与与双曲线有两个交点,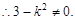
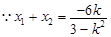 ,
,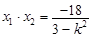 ,
,
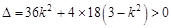 …………8分
…………8分
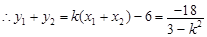 ,
,
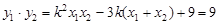
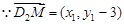 ,
,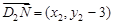 ,
,
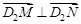
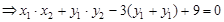
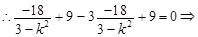
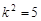 ,
,
满足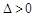 ,
,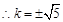 …………10分
…………10分
故所求直线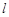 方程为
方程为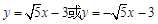 …………12分
…………12分

练习册系列答案
相关题目
 <1,xÎR }.
<1,xÎR }. ,求实数a的取值范围.
,求实数a的取值范围. (
( ,
, 为常数),且方程
为常数),且方程 有两个实根为
有两个实根为 .
. 的解析式;
的解析式; 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
, 为
为 上的点,且
上的点,且 ⊥平面
⊥平面
 ⊥平面
⊥平面
 的大小;
的大小; 到平面
到平面