题目内容
已知函数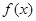
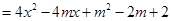 的图像与
的图像与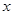 轴有两个交点
轴有两个交点
(1)设两个交点的横坐标分别为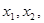 试判断函数
试判断函数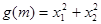 有没有最大值或最小值,并说明理由.
有没有最大值或最小值,并说明理由.
(2)若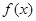
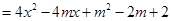 与
与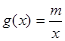 在区间
在区间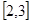 上都是减函数,求实数
上都是减函数,求实数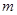 的取值范围.
的取值范围.
(1)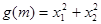 没有最大值也没有最小值;(2)
没有最大值也没有最小值;(2)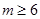 。
。
解析试题分析:由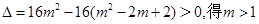 , 2分
, 2分
(1)
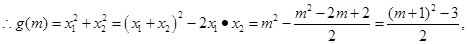 6分
6分
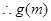 没有最大值也没有最小值 8分
没有最大值也没有最小值 8分
(2).依题意得: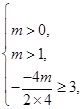 , 11分
, 11分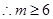 12分
12分
考点:本题主要考查二次函数的图象和性质,简单不等式组的解法。
点评:典型题,涉及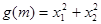 这类函数的求最值问题,注意运用韦达定理,简化解题过程。
这类函数的求最值问题,注意运用韦达定理,简化解题过程。

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
(本小题满分12分)探究函数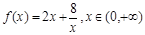 的最小值,并确定取得最小值时x的值.列表如下:
的最小值,并确定取得最小值时x的值.列表如下:
| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 16 | 10 | 8.34 | 8.1 | 8.01 | 8 | 8.01 | 8.04 | 8.08 | 8.6 | 10 | 11.6 | 15.14 | … |
(1)函数
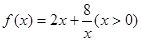 在区间(0,2)上递减;函数
在区间(0,2)上递减;函数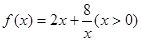 在区间 上递增.当
在区间 上递增.当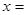 时,
时,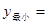 .
.(2)证明:函数
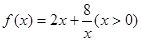 在区间(0,2)递减.
在区间(0,2)递减.(3)思考:函数
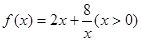 时,有最值吗?是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
时,有最值吗?是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)  ,若
,若 为定义在R上的奇函数,则(1)求实数
为定义在R上的奇函数,则(1)求实数 的值;(2)求函数
的值;(2)求函数 的不等式:
的不等式: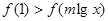
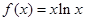 ,
,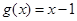 .
. 的单调区间;
的单调区间;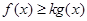 恒成立,求实数k的值;
恒成立,求实数k的值;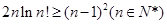 .(其中
.(其中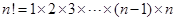 )
)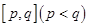 ,使得函数在区间
,使得函数在区间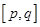 上的值域为
上的值域为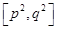 .
. 的图像经过点
的图像经过点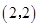 ,判断
,判断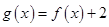
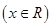 是否是和谐函数?
是否是和谐函数?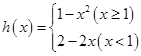 是否是和谐函数?
是否是和谐函数?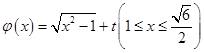 是和谐函数,求实数
是和谐函数,求实数 的取值范围.
的取值范围.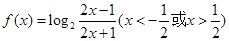 .
.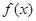 是奇函数;
是奇函数; 图象的一个对称中心.
图象的一个对称中心.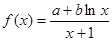 在点
在点 处的切线方程为
处的切线方程为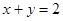 .
. ,
, 的值;
的值; 定义域内的任一个实数
定义域内的任一个实数 ,
,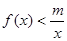 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 的最小值为1,且
的最小值为1,且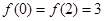 .
.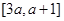 上不单调,求实数
上不单调,求实数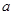 的取值范围;
的取值范围;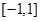 上,
上,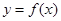 的图象恒在
的图象恒在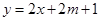 的图象上方,试确定实数
的图象上方,试确定实数 的取值范围.
的取值范围.