题目内容
【题目】计算
（1）已知f（x）=（x2+2x）ex ， 求f′（﹣1）；
（2）∫ 
cos2 
dx．
【答案】
（1）解：f′（x）=（2x+2）ex+ex（x2+2x）=（x2+4x+2）ex，
f′（﹣1）=﹣ 
（2）解： 
= 
= 
+ 
= 
，
∴ =
【解析】（1）求出原函数的导函数，然后在导函数中取x=﹣1得答案；（2）根据定积分的计算法则计算即可．
【考点精析】关于本题考查的基本求导法则和定积分的概念，需要了解若两个函数可导，则它们和、差、积、商必可导；若两个函数均不可导，则它们的和、差、积、商不一定不可导；定积分的值是一个常数，可正、可负、可为零；用定义求定积分的四个基本步骤：①分割；②近似代替；③求和；④取极限才能得出正确答案．
练习册系列答案
相关题目
【题目】大学生赵敏利用寒假参加社会实践，对机械销售公司7月份至11月份销售某种机械配件的销售量及销售单价进行了调查，销售单价x元和销售量y件之间的一组数据如表所示：
月份 | 7 | 8 | 9 | 10 | 11 |
销售单价x元 | 9 | 9.5 | 10 | 10.5 | 11 |
销售量y件 | 11 | 10 | 8 | 6 | 5 |
（1）根据7至11月份的数据，求出y关于x的回归直线方程；
（2）预计在今后的销售中，销售量与销售单价仍然服从（1）中的关系，若该种机器配件的成本是2.5元/件，那么该配件的销售单价应定为多少元才能获得最大利润？ 参考公式：回归直线方程 
=b 
+a，其中b=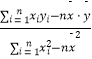 
．
参考数据： 
=392， 
=502.5．
